728x90
B-Spline
B-Splines
- Is it possible to achieve both $C^{2}$-continuity and local controllability?
- B-splines can do!
- Uniform cubic B-spline basis functions
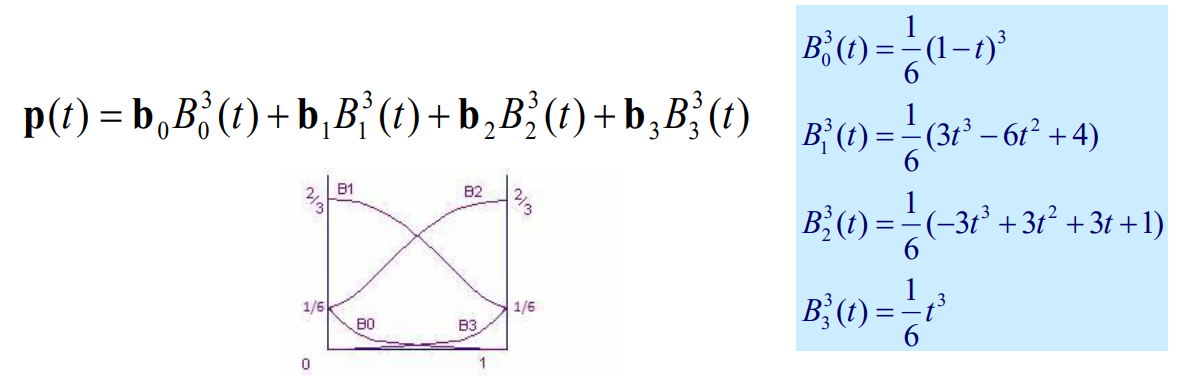
Uniform B-spline basis functions
- Bell-shaped basis function for each control points

- Overlapping basis functions
- Control points correspond to knot points

Uniform B-splines
 |
 |
- We have $(n+1)+2$ unknowns.
B-spline Properties
- Variation Diminishing
- $C^{2}$-continuity
- Local Controllability
Demo
B-spline basis functions
B-spline basis functions The equation for k-order B-spline with n+1 control points (P0 , P1 , ... , Pn ) is P(t) = ∑i=0,n Ni,k(t) Pi , tk-1 ≤ t ≤ tn+1 . In a B-spline each control point is associated with a basis function Ni,k which is gi
www.ibiblio.org
Summary
- Polynomial Interpolation
- Lagrange Polynomial
- Oscillation Problem
- Spline Interpolation
- Natural Cubic Spline
- $C^{2}$-continuity
- No Local Controllability
- Catmull-Rom Spline
- $C^{1}$-continuity
- Local Controllability
- B-Spline
- $C^{2}$-continuity
- Local Controllability
- Natural Cubic Spline
728x90
'Computer Graphics' 카테고리의 다른 글
| [Computer Animation] 애니메이션을 제작할 때 도움이 될 만한 사이트 (0) | 2022.06.23 |
|---|---|
| [Computer Animation] Quaternion Catmull-Rom Spline (0) | 2022.05.01 |
| [Computer Animation] De Casteljau Algorithm (0) | 2022.05.01 |
| [Computer Animation] Natural Cubic Spline (0) | 2022.05.01 |
| [Computer Animation] Catmull-Rom Spline (0) | 2022.05.01 |
| [Computer Animation] Bezier Curve & Bezier Spline (0) | 2022.05.01 |
| [Computer Animation] Keyframing and Splines (0) | 2022.05.01 |
| [Unreal Engine 4] 블루프린트 클래스(Blueprint Class)에 Static Mesh 연결하기 (0) | 2022.04.24 |

