728x90
Bezier Curve & Bezier Spline
Basic Functions
- A linear space of cubic polynomials
- Monomial basis $(t^{3}, t^{2}, t^{1}, t^{0}$
- $x(t) = a_{3}t^{3} + a_{2}t^{2} + a_{1}t + a_{0}$
- The coefficients $a_{i}$ do not give tangible(유형의) geometric meaning.
- Monomial basis $(t^{3}, t^{2}, t^{1}, t^{0}$
Bezier Control Points
- Control Points
- $b_{0}, b_{1}, b_{2}, b_{3}$
- Demo
Canvas Bézier Curve Example
blogs.sitepointstatic.com
Bezier Curve(베지어 곡선)
- Cubic polynomial in Bernstein Bases(번스타인 기초)
- $p(t) = b_{0}B_{0}^{3}(t) + b_{1}B_{1}^{3}(t) + b_{2}B_{2}^{3}(t) + b_{3}B_{3}^{3}(t)$ $(0 ≤ t ≤ 1)$
- Bernstein Basis Functions

Cubic Bernstein Basis Functions

Bernstein Basis Functions

- $p(t)$ is a linear combination of points $b_{0}, b_{1}, b_{2},$ and $b_{3}$

- Derivative(미분) of $p(t)$
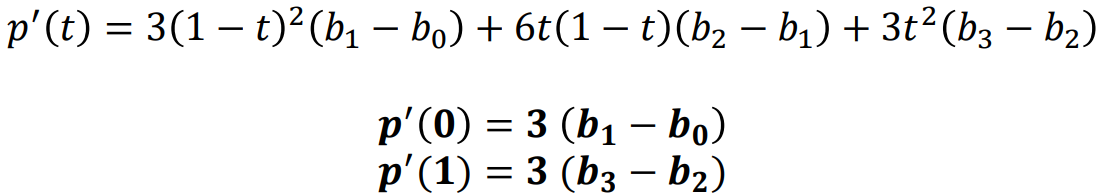
Properties of Cubic Beizer Curves
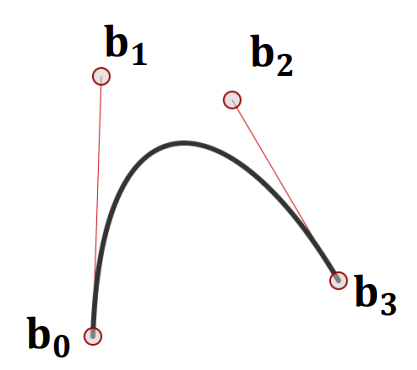
- End point interpolation
- $p(0) = b_{0}$
- $p(1) = b_{3}$
- The tangent vectors to the curve at the end points are coincident with the first and last edges of the control point polygon.
- $p'(0) = 3(b_{1} - b_{0})$
- $p'(1) = 3(b_{3} - b_{2})$
- Invariance under Affine Transformation
- Partition of unity of Bernstein Basis functions
- The curve is contained in the Conven Hull of the control polygen
- Variation Diminishing
- The curve in 2D space does not oscillate about any straight line more often than the control point polygon.

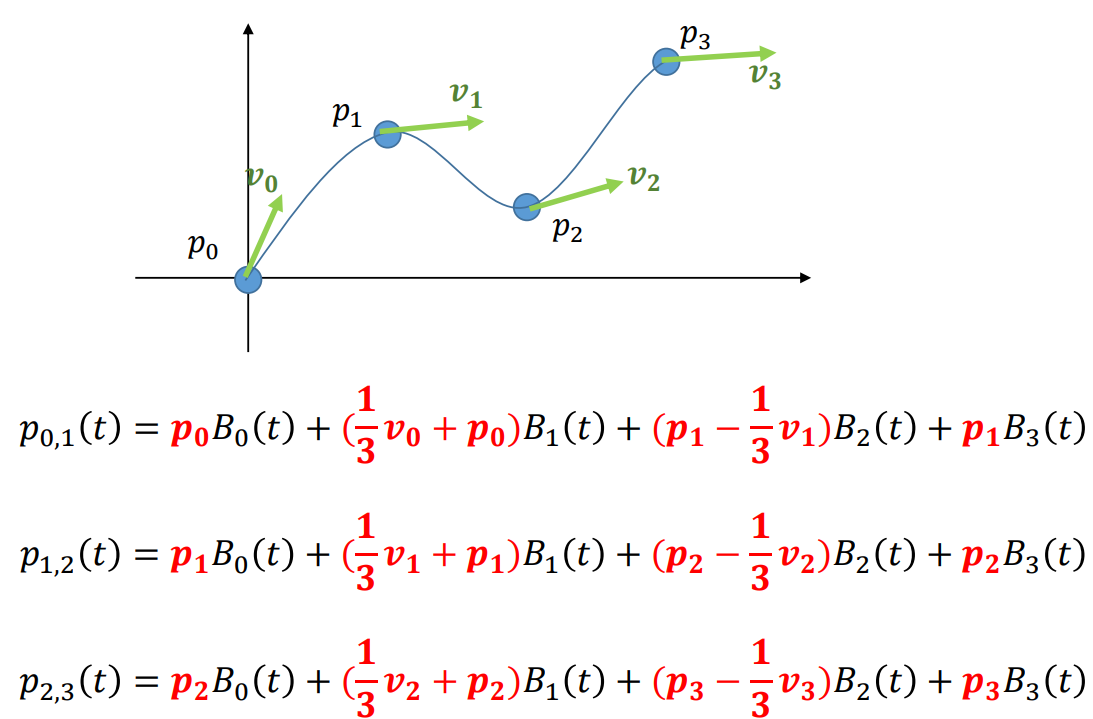
Bezier Spline
Beizer Splines
- When four key points and tangent conditions are given,

What is the First Bezier Curve?
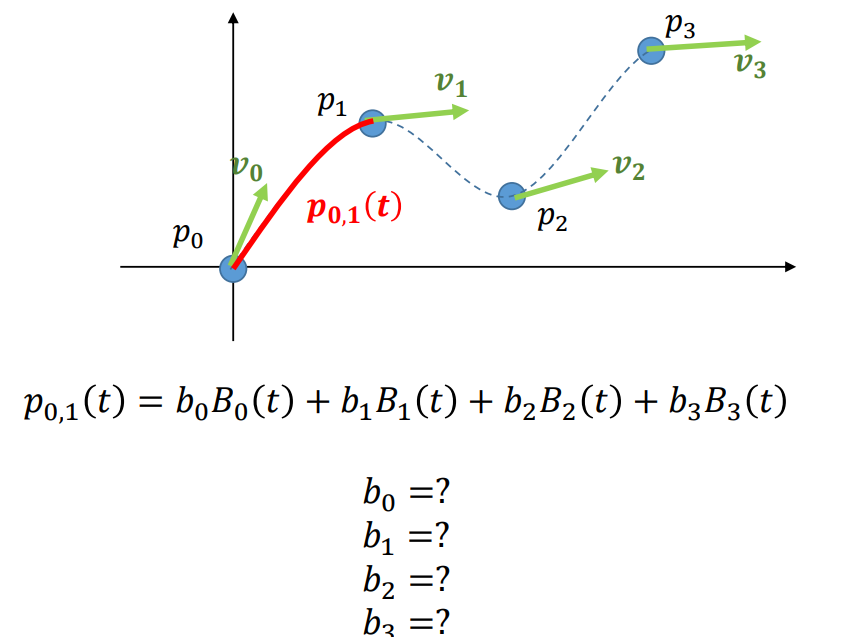
First Bezier Curve?

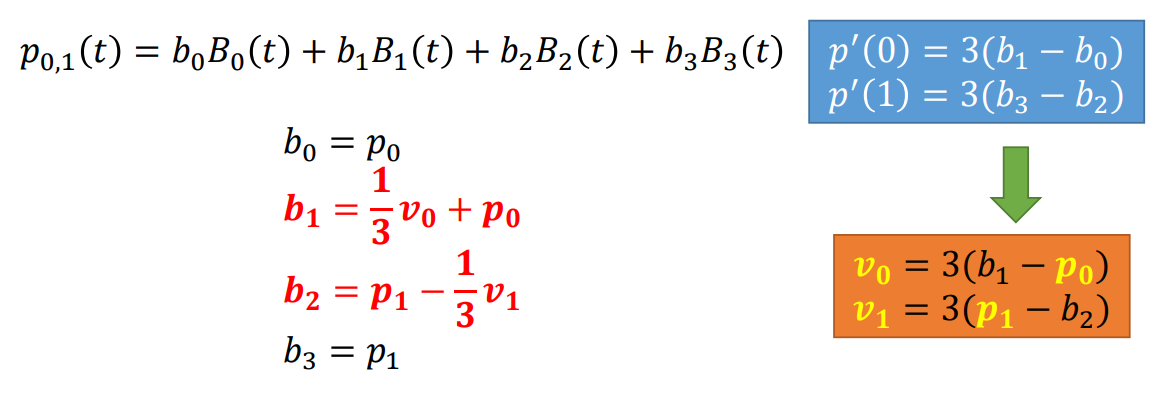
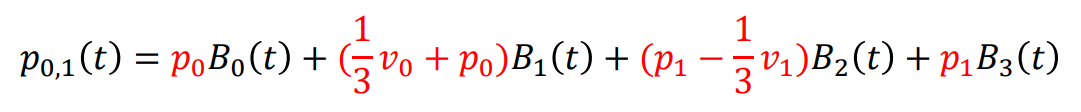
Bezier Spline
728x90
'Computer Graphics' 카테고리의 다른 글
| [Computer Animation] De Casteljau Algorithm (0) | 2022.05.01 |
|---|---|
| [Computer Animation] B-Spline (0) | 2022.05.01 |
| [Computer Animation] Natural Cubic Spline (0) | 2022.05.01 |
| [Computer Animation] Catmull-Rom Spline (0) | 2022.05.01 |
| [Computer Animation] Keyframing and Splines (0) | 2022.05.01 |
| [Unreal Engine 4] 블루프린트 클래스(Blueprint Class)에 Static Mesh 연결하기 (0) | 2022.04.24 |
| [Unreal Engine 4] 새로운 월드 생성 & 기본 환경 설정 (0) | 2022.04.16 |
| [Computer Animation] Slerp(Spherical Linear Interpolation) (0) | 2022.04.10 |

