[Computer Animation] Slerp(Spherical Linear Interpolation)

Slerp(Spherical Linear Interpolation)

Interpolation betwee two orientations, $o_{a}$ and $o_{b}$?

• $o_{a}$ and $o_{b}$ can be represented by 
  • Euler-angles
  • 3x3 matrices
  • quaternions
• How can them be interpolated?
• Is the linear interpolation applicable?

 

When the axis-angle is known, $o_{a} → o_{b}$

 

Rotation between two orientations?

• Rotation between two SO(3) matrices, $m_{a}$ and $m_{b}$
  • $m_{r} = m_{b}m_{a}^{-1}$
• Rotation between two quaternions, $q_{a}$ and $q_{b}$
  • $q_{r} = q_{b}q_{a}^{-1}$

 

Quaternion → Axis-Angle

 

Rotation Matrix → Axis-Angle

 

Interpolation $m_{a} → m_{b}$

 

 

Interpolation $q_{a} → q_{b}$

 

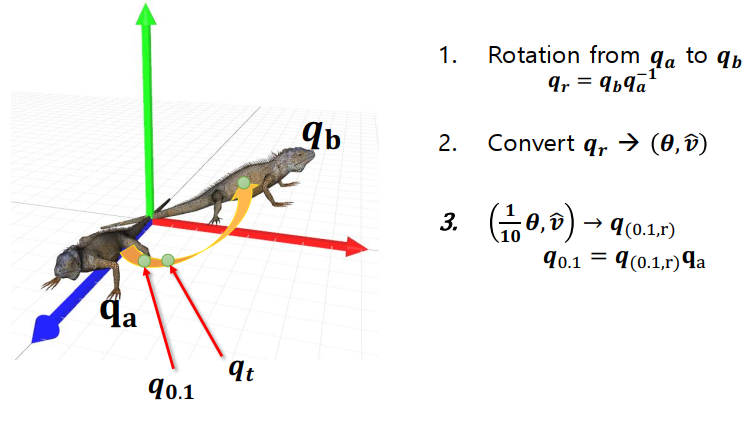
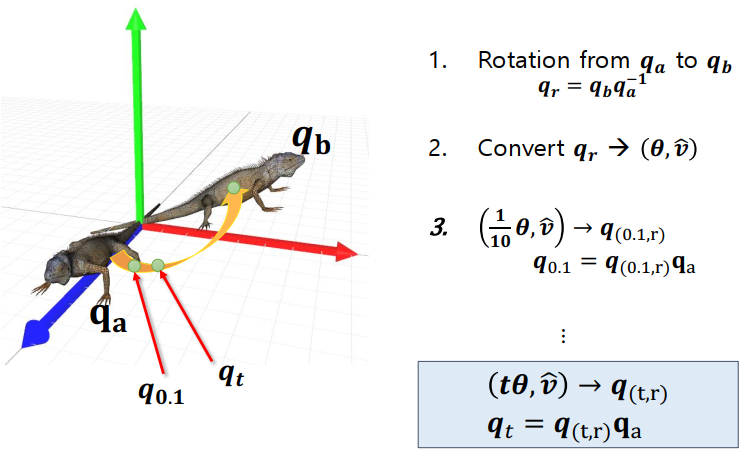
Alternative Method

 

 

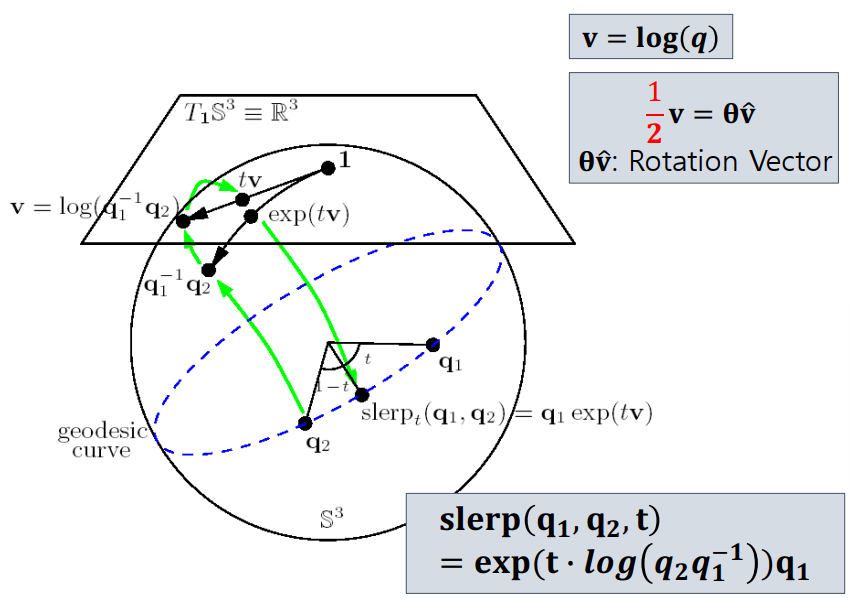
Quaternion Slerp

2D Complex Number Form

 

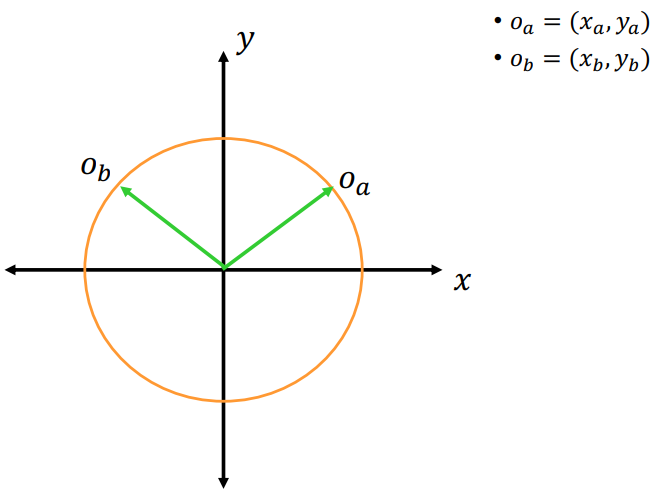
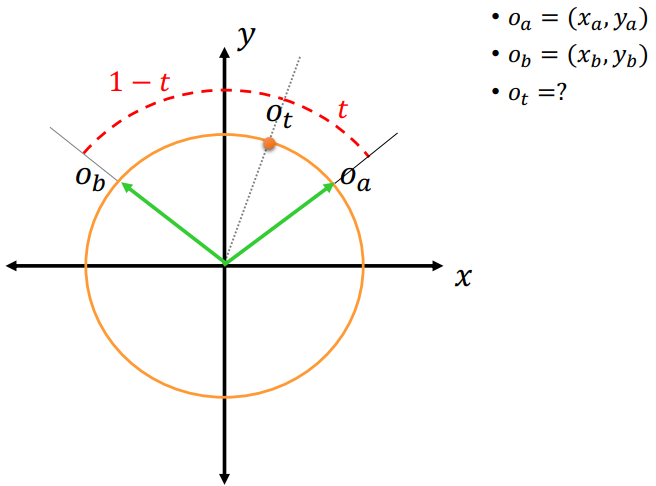
2D Spherical Interpolation

 

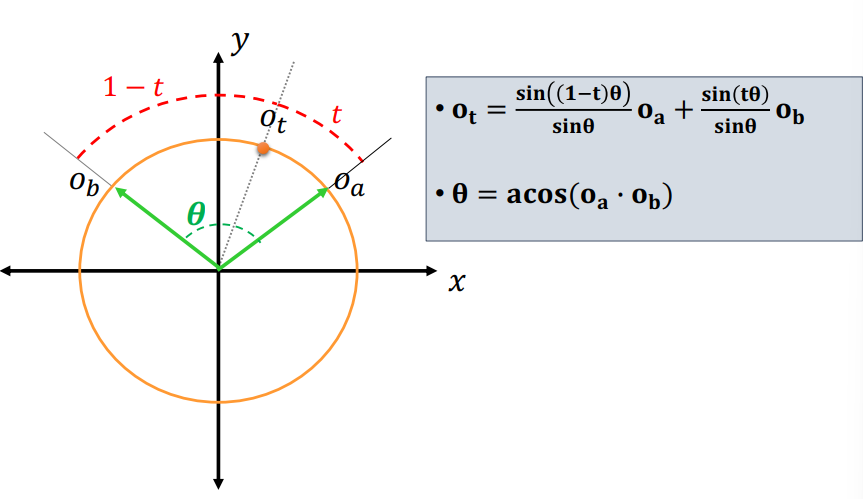
Spherical Linear Interpolation

• SLERP [Shoemake 1985]
  • Linear Interpolation of two quaternions

 

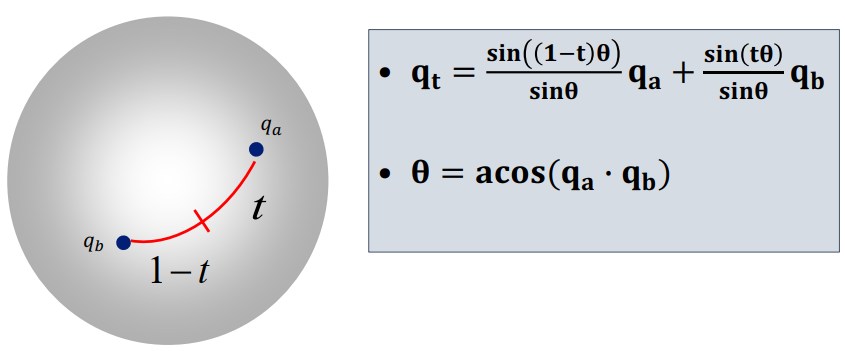
Antipodal Equivalence Problem

 

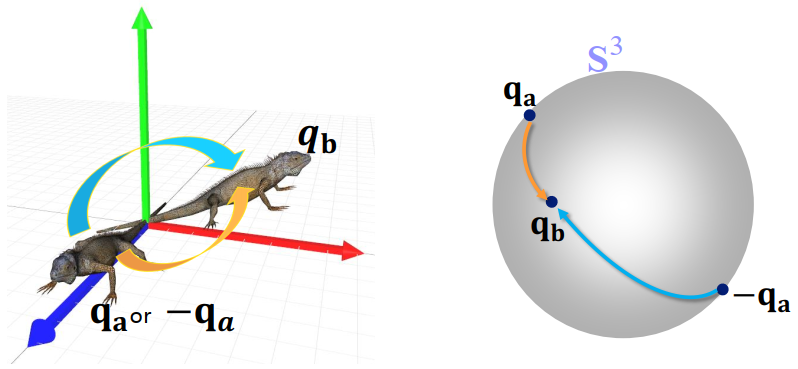
• In gerneral, the shorter pass is better
• You should test both $q_{a}$ and $-q_{a}$ , and choose one

 

Rotation Matrix vs. Unit Quaternion

• Equivalent in many aspects
  • No singularity
  • Exp & Log
  • Special tangent space
• Why quaternions?
  • Fewer parameters
  • Simpler algebra
  • Easy to fix numerical error
• Why rotation matrices?
  • One-to-one correspondence
  • Handle rotation and translation in a uniform way
    • Eg) 4x4 homogeneous matrices