728x90
2D Rotation and Orientation
Orientation vs. Rotation
- Rotation
- Circular movement.
- Orientation
- The state of being oriented.
- Given a coordinate system, the orientation of an object can be represented as a rotation from a reference pose.
- Analogy
- (point : vector) is similar to (orientation : rotation)
- Both represent a sort of (state : movement)
Representations for 2D rotations and orientations
- Turning angles.
- Complex numbers.
- Rotation matrices.
Turning Angles
Rotate by a turning angle, $\theta˚$
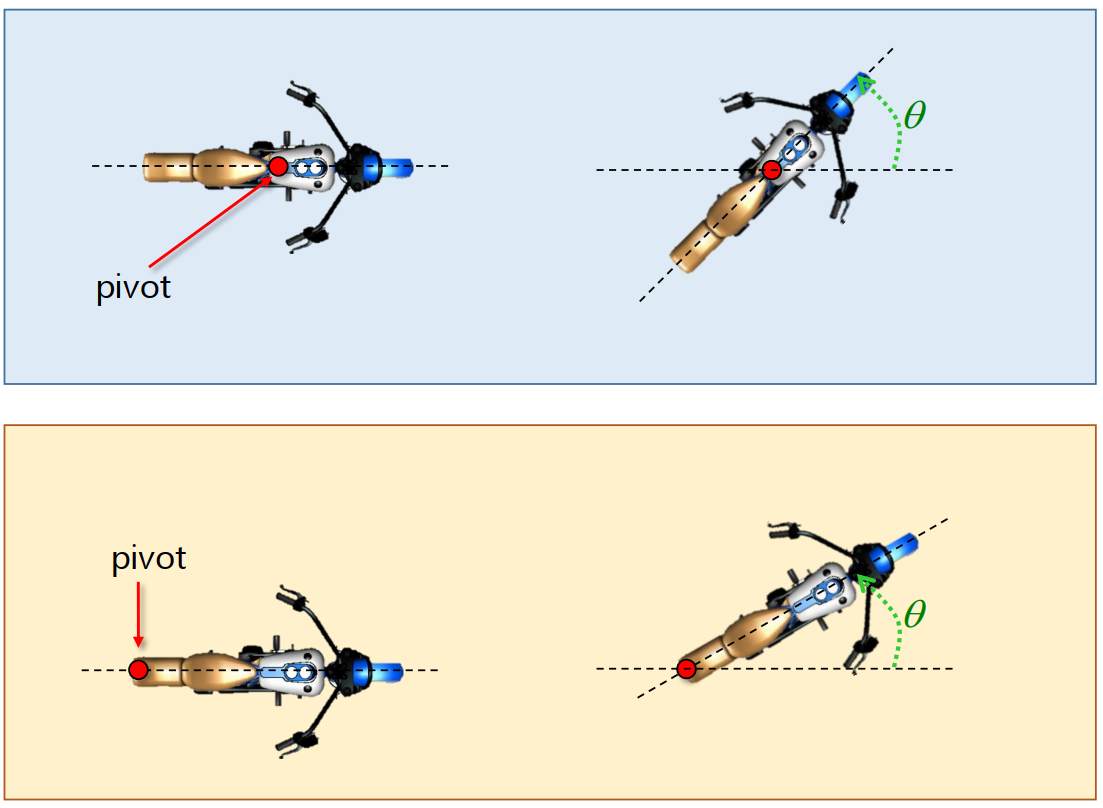
Turning Angles for 2D Rotations
Rotation between two states
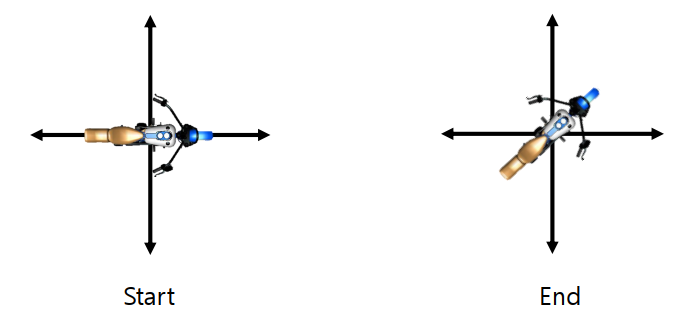
Turning Angle from the Reference pose
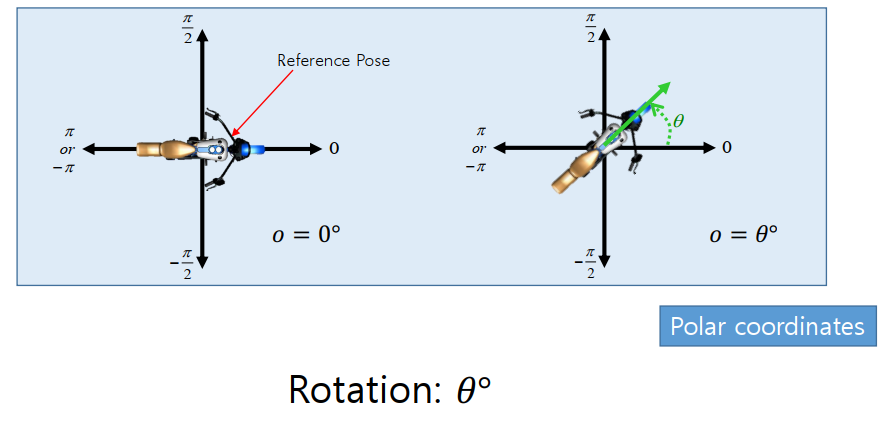
- Different rotational movements can result in the same final orientation
- Turn 45 degree counter-clockwise
- Turn -315 degree clockwise
- Turn 405 degree counter-clockwise
Reference poses

Turning Angles for 2D Orientations?
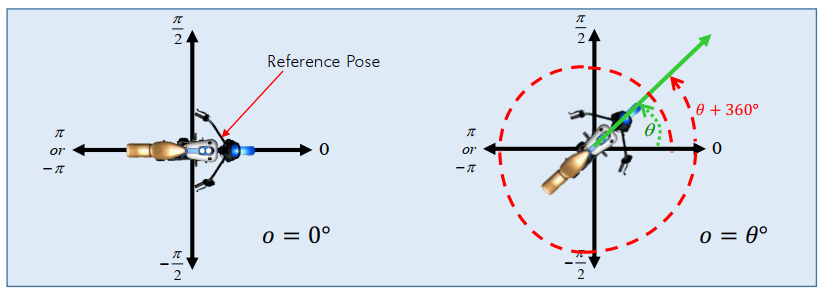
Orientations by turning angles
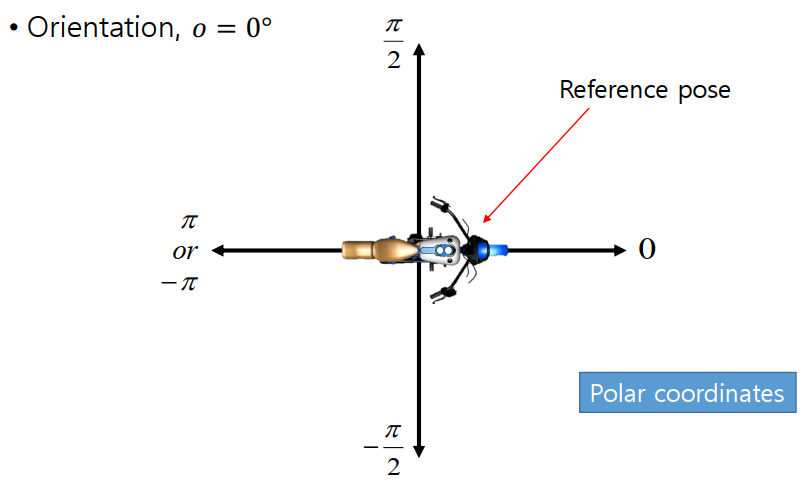
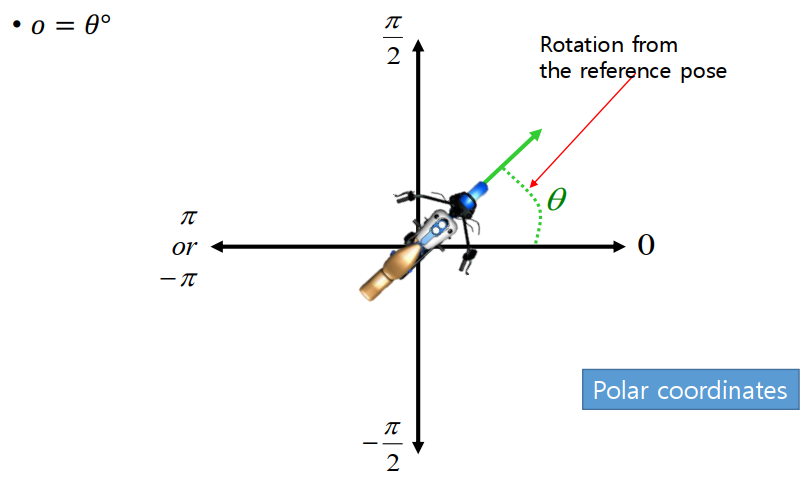
One-to-one mapping between angles and orientations.
What is rotation between $o_{1}$ and $o_{2}$?
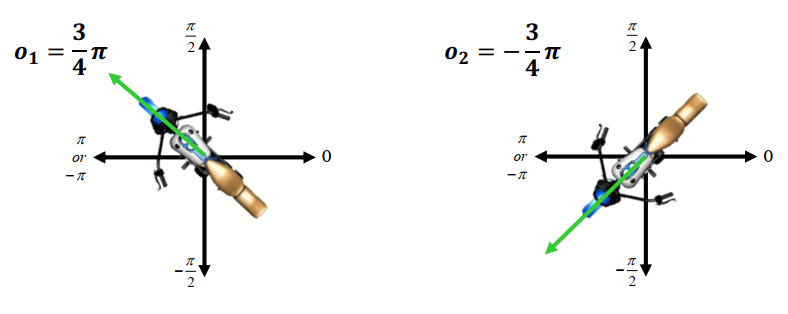

- From $o_{1}$ to $o_{2}$ : $o_{2} - o_{1} = - \frac{3}{2} \pi$
- From $o_{2}$ to $o_{1}$ : $o_{1} - o_{2} = \frac{3}{2} \pi$
- How can the shorter rotation be calculated?
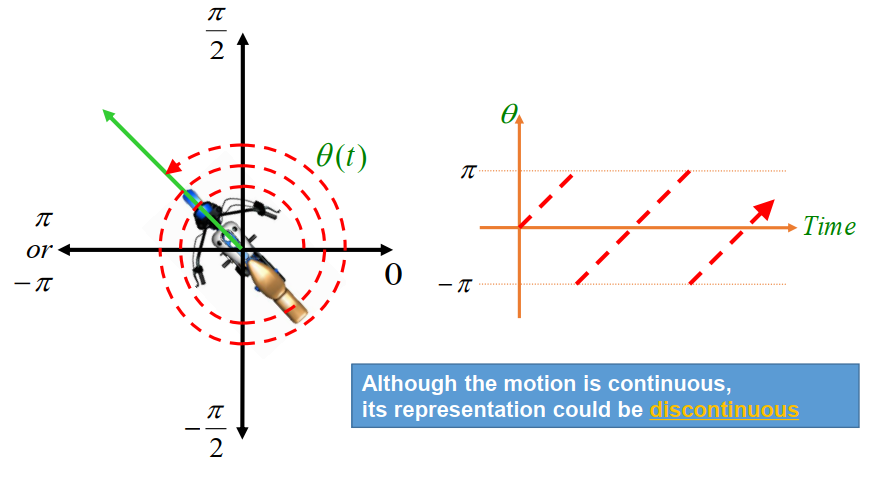
Many-to-one mapping between angles and orientations.
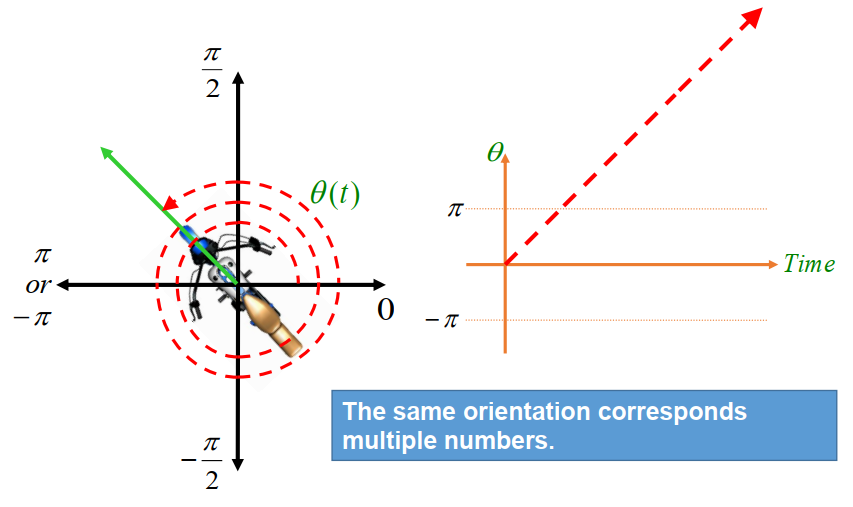
Which one is better for 2D orientation?
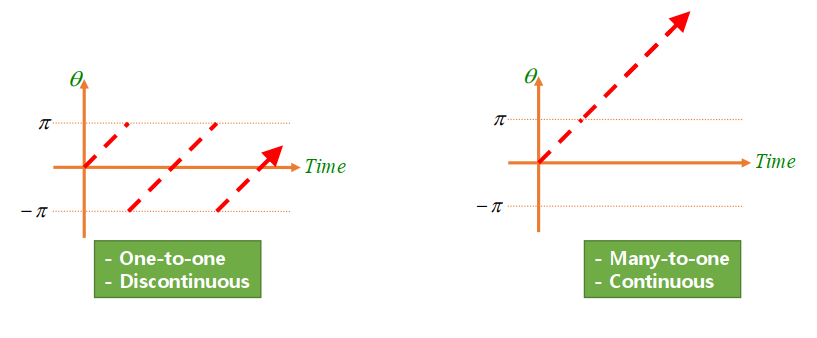
- Can it be one-to-one and continuous at the same time?
Complex Numbers
Extra Parameter
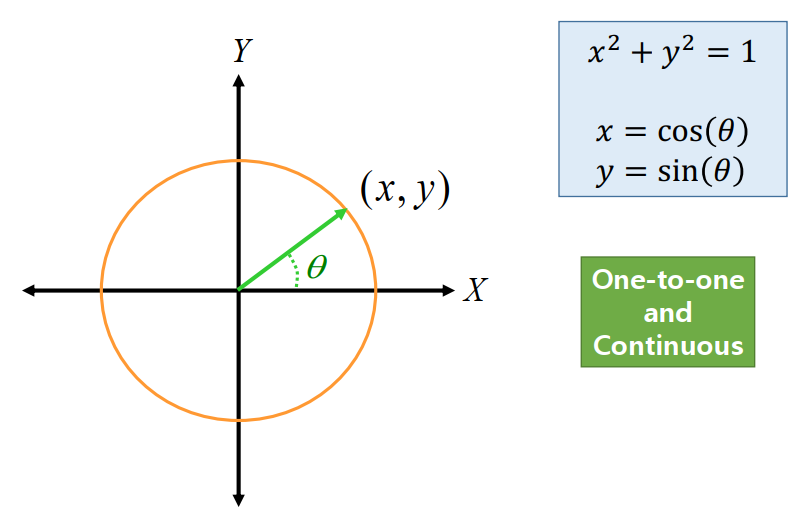
Complex number form
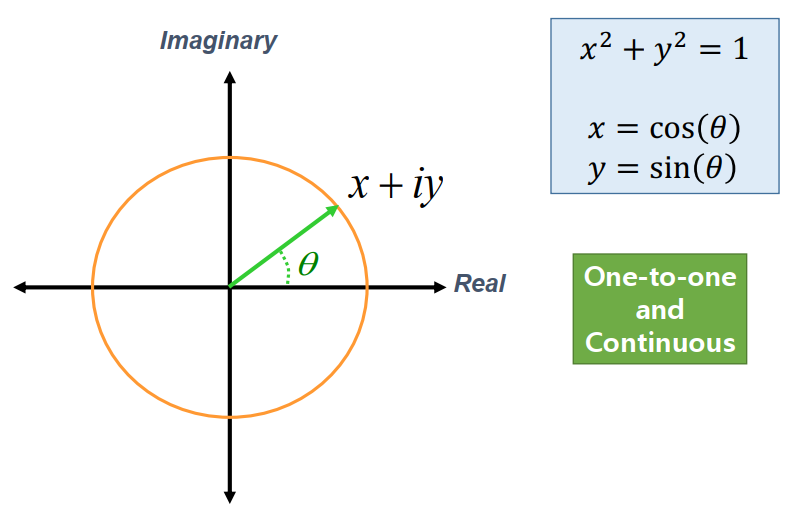
Circle group (or SO(2) group)
- The circle group is a group of all complex numbers with absolute value 1.
- $\sqrt {x^{2} + y^{2}} = 1$
- One element in the circle group corresponds to one unique 2D orientation.
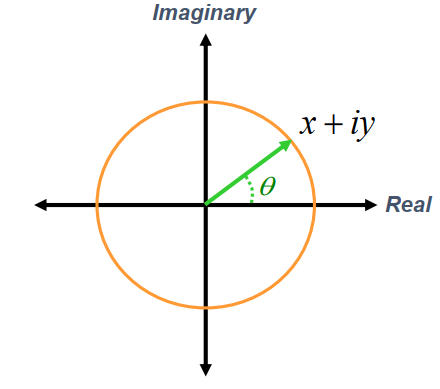
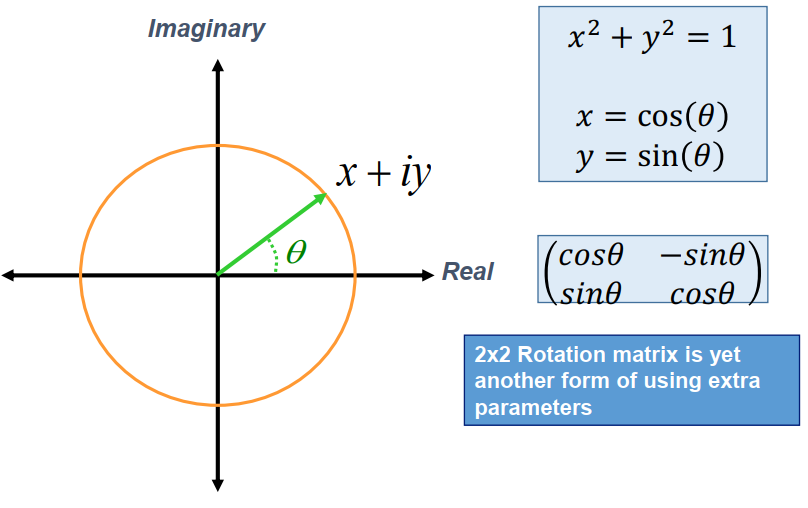
2×2 Matrix form
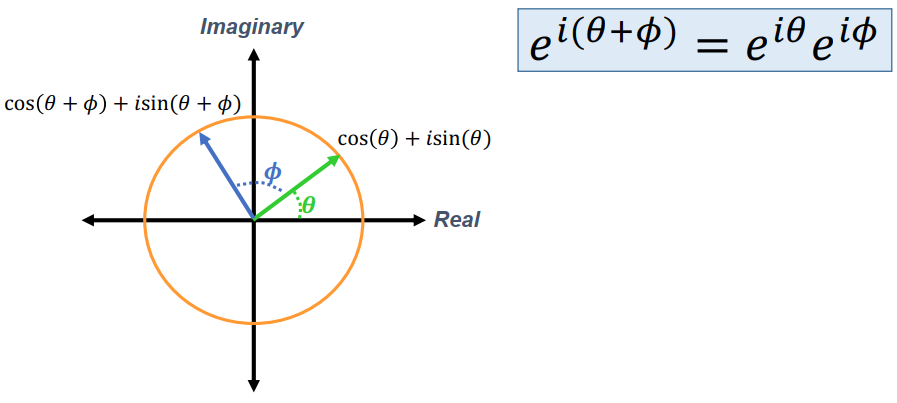
Exponential form of complex numbers

Rotation composition
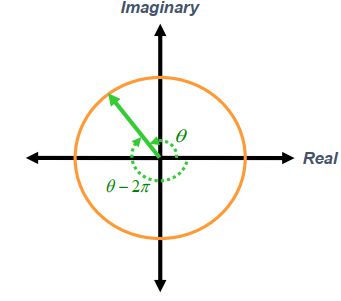
2D rotations by complex numbers?
- Complex numbers are good for representing 2D orientations(one-to-one mapping), but inadequate for 2D rotations.
- A complex number cannot distinguish different rotational movements that result in the same final orientation.
- Turn 120 degree counter-clockwise
- Turn -240 degree clockwise
- Turn 480 degree counter-clockwise
Conclusion
2D Rotation
- The consequence of any 2D rotational movement can be uniquely represented by a turning angle.
- A turning angle is independent of the choice of the reference orientation.
2D Orientation
- The non-singular parameterization of 2D orientations requires extra parameters.
- Eg) Complex numbers, 2×2 rotation matrices
- The parameterization is dependednt on the choice of the reference orientation.
2D Slerp(Sherical Linear Interpolation)
Two orientations, $o_{a}$ and $o_{b}$
- $o_{a} = (x_{a}, y_{a})$
- $o_{b} = (x_{b}, y_{b})$
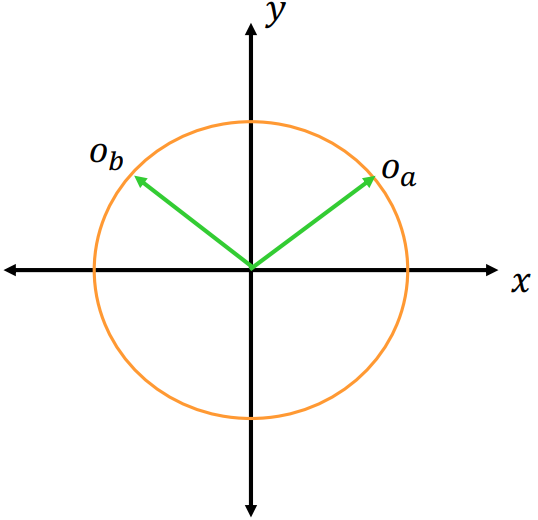
Interpolation between $o_{a}$ and $o_{b}$
- $o_{a} = (x_{a}, y_{a})$
- $o_{b} = (x_{b}, y_{b})$
- $o_{t} = ?$
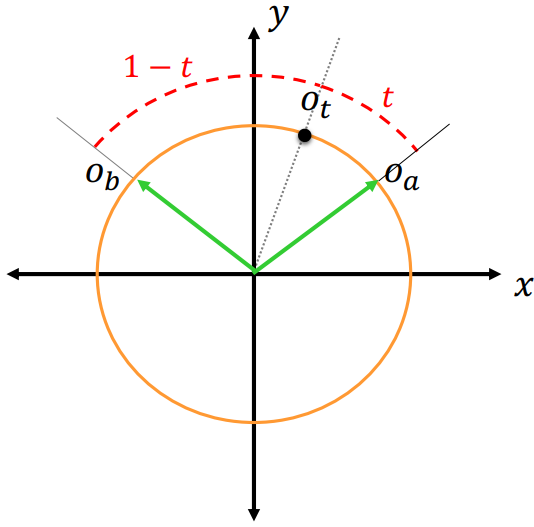
Linear Interpolation?
- $o'_{t} = o_{a} + t(o_{b} - o_{a}) = (1 - t)o_{a} + to_{b}$
- $o'_{t} ≠ o_{t}$
- $o'_{t} \notin SO(2)$
- Linear interpolation results a 2D vector that is not in the circular group.
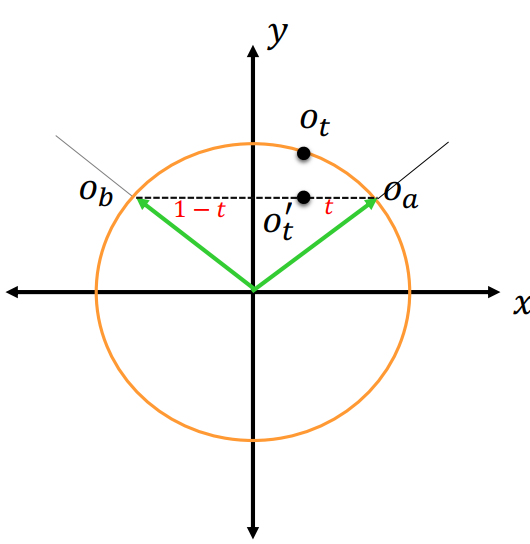
2D Spherical Interpolation

728x90
'Computer Graphics' 카테고리의 다른 글
| [Unreal Engine 4] 블루프린트 클래스(Blueprint Class)에 Static Mesh 연결하기 (0) | 2022.04.24 |
|---|---|
| [Unreal Engine 4] 새로운 월드 생성 & 기본 환경 설정 (0) | 2022.04.16 |
| [Computer Animation] Slerp(Spherical Linear Interpolation) (0) | 2022.04.10 |
| [Computer Animation] 3D Rotation and Orientation (0) | 2022.04.10 |
| [Computer Animation] Linear Interpolation (0) | 2022.03.26 |
| [Computer Animation] Geometric Transformations (0) | 2022.03.26 |
| [Computer Animation] Vector Operations (0) | 2022.03.15 |
| [Computer Animation] Point and Vector (Affine Geometry) (0) | 2022.03.15 |

