728x90
Point and Vector (Affine Geometry)
Animation
Function of time

Movement

1D Space
| Uniform Speed | Non-Uniform Speed |
 |
 |
2D or 3D Space
- Cartesian Coordinate System(데카르트 좌표계) 를 사용하여 표현한다.
 |
 |
- 함수가 만들어지는 절차
| Sampling Global Points |  |
| In a New Coordinates System |  |
| Sampling Difference Vectors |  |
| In a New Coordinates System |  |
| Function |  |
Points and Vectors
Points and Vectors

- A Point is a position specified with coordinate values.
- A Vector is specified as the difference between two points.
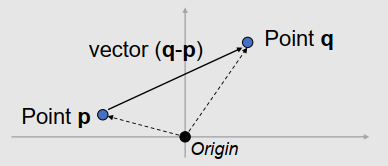
- If an Origin is specified, then a point can be represented by a vector from the origin.
- A Point is not a vector in Coordinate-Free concepts.
Vector and Affine Spaces
- Vector Space(벡터 공간)
- Includes vectors and related operations.
- No points
- Affine Space(아핀 공간)
- Superset of vector space.
- Includes vectors, points and related operations.
Vector Spaces
- A Vector Space consists of
- Set of Vectors, together with
- Two Operations
- Addition of vectors(벡터의 합)
- Multiplication of vectors by Scalar Numbers. (스칼라 수에 의한 벡터의 곱)
- A Linear Combination(선형 결합) of vectors is also a vector.
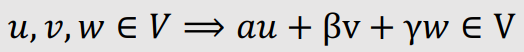
Affine Spaces
- A Affine Space consists of
- Set of Points, An Associated Vector Space, and
- Two more operations
- The difference between two points
- The addition of a vector to a point
- They are Coordinate-Free Geometric Operations.
Coordinate-Free Operations
Example of Coordinate-Dependence
- 두 위치의 합(Sum)은 얼마일까?
If you assume coordinates, ...

- 합은 $(x_{1} + x_{2}, y_{1} + y_{2})$ 가 된다.
- 정답일까?
- 기하학적으로 의미가 있을까?
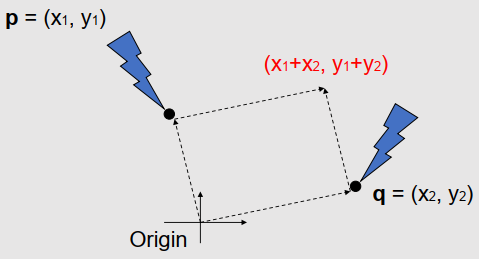
- Vector Sum
- $(x_{1}, y_{q})$ and $(x_{2}, y_{2})$ are considered as vectors from the origin to $p$ and $q$, respectively.
If you select a different origin, ...
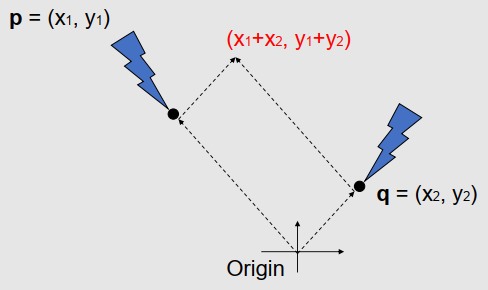
- If you choose a different coordinate frame, you will get a different result.
Coordinate-Free Geometric Operations
- Addition
- Subtraction
- Scalar Multiplication
- Linear Combination
- Affine Combination
Addition
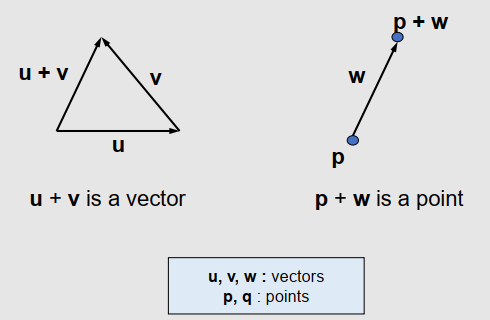
- Vector + Vector = Vector
- Point + Vector = Point
Subtraction
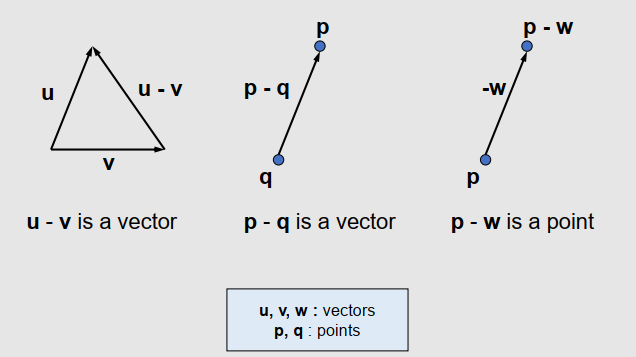
- Vector - Vector = Vector
- Point - Point = Vector
- Point - Vector = Point
Scalar Multiplication

- Scalar × Vector = Vector
- 1 × Point = Point
- 0 × Point = Vector
- c × Point = (undefined) if (c ≠ 0, 1)
Linear Combination of Points

Examples
- (p + q) / 2 : Midpoint of line pq
- (p + q) / 3 : Can you find a geometric meaning ?
- 기하학적 의미가 없다.
- (p + q + r) / 3 : Center of gravity of Δpqr
- (p/2 + q/2 - r) : A Vector from r to the midpoint of q and p
Summary

728x90
'Computer Graphics' 카테고리의 다른 글
| [Computer Animation] Slerp(Spherical Linear Interpolation) (0) | 2022.04.10 |
|---|---|
| [Computer Animation] 3D Rotation and Orientation (0) | 2022.04.10 |
| [Computer Animation] 2D Rotation and Orientation (0) | 2022.04.03 |
| [Computer Animation] Linear Interpolation (0) | 2022.03.26 |
| [Computer Animation] Geometric Transformations (0) | 2022.03.26 |
| [Computer Animation] Vector Operations (0) | 2022.03.15 |
| [Computer Animation] History of Animation (0) | 2022.03.08 |
| [Computer Animation] Computer Animation (0) | 2022.03.03 |

