1. 집합(Set)

*1. 집합(Set)

 

집합은 확률과 통계를 학습하는 데 있어 기본적으로 필요한 개념이다.

따라서 확률과 통계를 배우기에 앞서 집합에 대한 기본적인 개념과 성질에 대한 이해가 필요하다.

 

1. 집합의 의미

- 집합(Set) : 주어진 조건에 의해 그 대상을 명확하게 구별할 수 있는 대상들의 모임

- 원소(Element) : 집합을 이루는 개개의 대상

- 예)

(명제1) '멋진 남학생과 아름다운 여학생의 모임' -> 집합이 아니다.  (명제2) '안경을 낀 학생들의 모임' -> 집합이다.

 

- 보편적으로 집합은 대문자 알파벳 A, B 등으로 나타내고, 원소는 소문자 알파벳 a, b 등으로 나타낸다.

- 원소 a가 집합 A에 포함되는 관계는 다음과 같이 표현한다.

 

 

- 원소 b가 집합 B에 포함되지 않는 관계는 다음과 같이 표현한다.

 

 

- 집합 A를 나타낼 때는 다음과 같이 중괄호 기호( { } )를 이용하여 나타낸다.

- 이와 같이 집합을 이루는 모든 원소를 나열하여 표현하는 방법을 원소나열법(Tabular Form)이라고 한다.

 

 

- 또는 다음과 같이 조건을 이용하여 집합을 나타내기도 하는데, 이와 같이 표현하는 방법을 조건제시법(Set-Builder Form)이라고 한다.

 

A = {x | x는 짝수, 2 ≤ x ≤ 6}

 

- 전체집합(Universal Set)은 모든 원소들의 집합을 의미하며 U 로 나타낸다.

- 집합 A를 구성하는 원소의 개수가 유한개이면, 집합 A를 유한집합(Finite Set)이라 하고, 그렇지 않은 집합을 무한집합(Infinite Set)이라 한다.

- 무한집합 A의 원소의 개수를 셈할 수 있으면 집합 A를 가산집합(Countable Set)이라 하고 그렇지 않은 집합을 비가산집합(Uncountable Set)이라 한다.

- 원소가 하나도 없는 집합을 공집합(Empty Set)이라 하고, 로 나타낸다.

- 두 집합 A와 B에 대해 집합 A의 모든 원소가 집합 B에 속할 때, 집합 A를 집합 B의 부분집합(Subset)이라 하고 다음과 같이 나타낸다.

 

 

- 그리고 집합 A가 집합 B의 부분집합이 아닌 경우에는 다음과 같아 나타낸다.

 

  

 

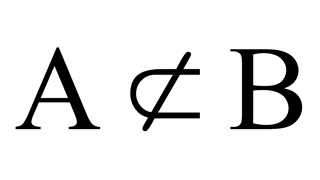
- 다음과 같은 두 집합을 서로 같다(Equal)고 하고, A = B 로 나타낸다. (서로 같지 않은 두 집합은 A ≠ B 로 나타낸다.)

 

 

- A ⊂ B 를 벤 다이어그램(Venn Diagram)으로 나타내면 다음과 같다.

 

 

 

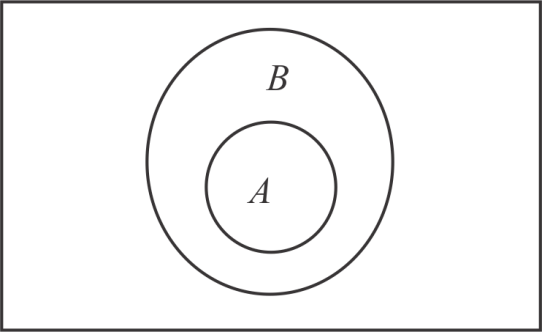
2. 여러 가지 집합

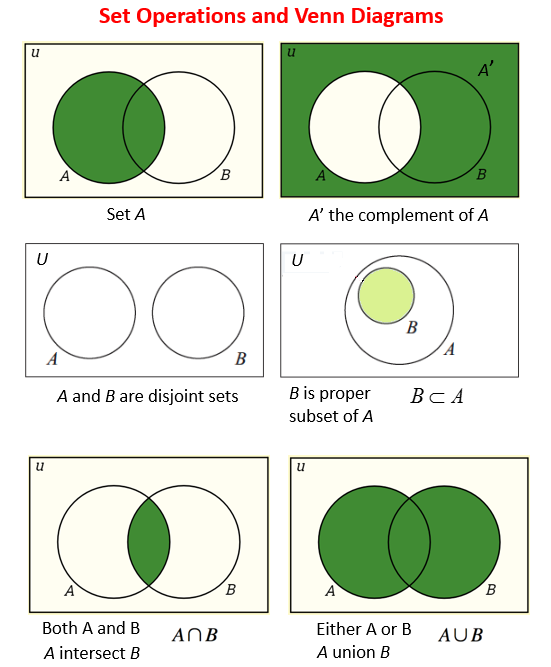
■ 교집합(Intersection of Sets)

- 두 집합 A와 B안에 모두 포함된 원소로 구성된 집합을 A와 B의 교집합(Intersection of Sets)이라고 하며, 다음과 같이 정의한다.

 

 

- 특히 다음과 같이 공통인 원소를 갖지 않는 두 집합을 A와 B의 서로소(Disjoint)라고 한다.

 

 

■ 합집합(Union of Sets)

- 집합 A 또는 B의 원소들로 구성된 집합을 A와 B의 합집합(Union of Sets)이라 하며, 다음과 같이 정의한다.

 

 

■ 차집합(Difference of Sets)

- 집합 A 안에는 포함되지만, 집합 B 안에는 포함되지 않는 원소로 구성된 집합을 집합 A와 B의 차집합(Difference of Sets)이라 하며, 다음과 같이 정의한다.

 

 

■ 여집합(Complementary Set)

- 집합 A안에 포함되지 않는 모든 원소로 구성된 집합을 A의 여집합(Complementary Set)이라 하며, 다음과 같이 정의한다.

 

 

- 여러 가지 집합의 벤 다이어그램

 

 

3. 집합의 성질

- 전체집합 U와 집합 A, B, C에 대해 다음과 같은 기본적인 집합 연산이 성립한다.

- 합집합과 교집합은 교환 법칙(Commutative Property)와 결합 법칙(Associative Property)이 성립한다.

 

■ 합집합의 성질

 

 

■ 교집합의 성질

 

 

■  여집합의 성질

 

■ 분배 법칙(Distributive Property)

 

 

■ 드 모르간의 법칙(De Morgan's Laws)

 

---

 

내용 출처 : 확률과 통계 입문(이재원 저, 한빛아카데미)