728x90
너비 우선 탐색(BFS, Breadth-First Search)
- 시작 정점을 경계(Frontier)에 추가하는 것으로 시작함.
- 경계는 이전에 방문했던 정점들 에 의해 구성됨.
- 현재 경계에 인접한 정점을 반복적으로 탐색함.
- 시간 복잡도 :
O(V + E)V: 정점의 개수E: 에지의 개수
- 모든 정점에 대해 자식 정점을 손자 정점보다 먼저 방문한다 는 점이 중요한 특징
- BFS를 구현할 경우, 보통 경계를 별도의 자료구조로 만들어서 명시적으로 사용하지는 않음.
- 대신 정점 ID를 큐(Queue) 에 저장하여 시작 정점과 가까운 정점을 멀리 있는 정점보다 먼저 방문할 수 있도록 구현함.
동작 과정
①
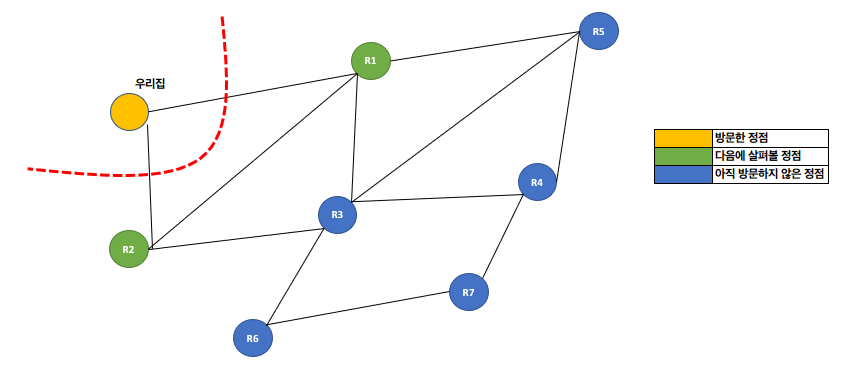
- 먼저 시작점인
우리집정점을 방문함. - 빨간색 점선 : 현재 경계
- 인접한 정점으로
R1과R2가 있음.
- 인접한 정점으로
②
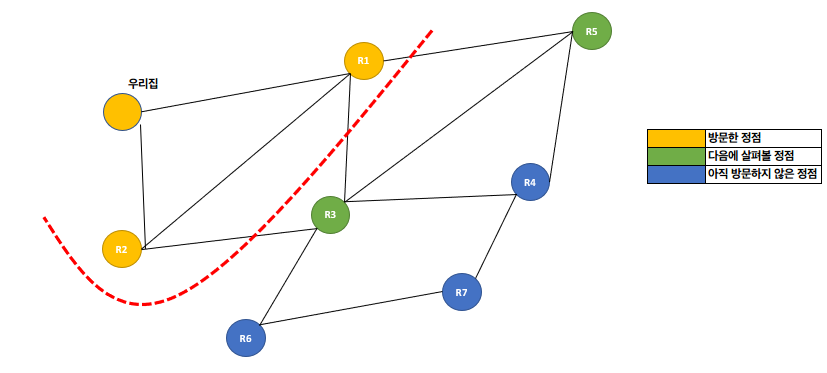
R1과R2정점을 방문한 후의 BFS 상태R1과R2는 어느 것을 먼저 방문해도 상관없음.- 시작 정점과 같은 거리에 있는 정점들의 방문 순서는 임의로 정해도 됨.
- 시작 정점에서 멀리 있는 정점보다 가까운 정점을 먼저 방문해야 한다 는 점이 중요함.
③
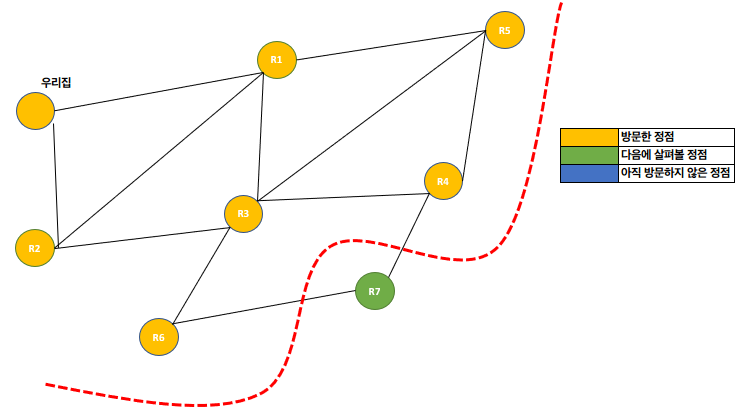
R3와R5,R4와R6정점 방문 후의 BFS 상태- 전체 그래프를 순회하기 직전의 모습
코드
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <map>
#include <queue>
using namespace std;
template <typename T>
struct Edge {
unsigned src;
unsigned dst;
T weight;
};
template <typename T>
class Graph {
public:
// N개의 정점으로 구성되 그래프
Graph(unsigned N) : V(N) {}
// 그래프의 정점 개수 반환
auto vertices() const { return V; }
// 전체 에지 리스트 반환
auto& edges() const { return edge_list; }
// 정점 v에서 나가는 모든 에지를 반환
auto edges(unsigned v) const {
vector<Edge<T>> edges_from_v;
for (auto& e : edge_list) {
if (e.src == v) {
edges_from_v.emplace_back(e);
}
}
return edges_from_v;
}
void add_edge(Edge<T>&& e) {
// 에지 양 끝 정점 ID가 유효한지 검사
if (e.src >= 1 && e.src <= V && e.dst >= 1 && e.dst <= V) {
edge_list.emplace_back(e);
}
else {
cerr << "에러: 유효 범위를 벗어난 정점!" << endl;
}
}
// 표준 출력 스트림 지원
template <typename U>
friend ostream& operator<< (ostream& os, const Graph<U>& G);
private:
unsigned V; // 정점 개수
vector<Edge<T>> edge_list;
};
template <typename U>
ostream& operator<< (ostream& os, const Graph<U>& G) {
for (unsigned i = 1; i < G.vertices(); i++) {
os << i << ":\t";
auto edges = G.edges(i);
for (auto& e : edges) {
os << "{" << e.dst << ": " << e.weight << "}, ";
}
os << endl;
}
return os;
}
template <typename T>
auto create_reference_graph() {
Graph<T> G(9);
map<unsigned, vector<pair<unsigned, T>>> edge_map;
edge_map[1] = { {2, 0}, {5, 0} };
edge_map[2] = { {1, 0}, {5, 0}, {4, 0} };
edge_map[3] = { {4, 0}, {7, 0} };
edge_map[4] = { {2, 0}, {3, 0}, {5, 0}, {6, 0}, {8, 0} };
edge_map[5] = { {1, 0}, {2, 0}, {4, 0}, {8, 0} };
edge_map[6] = { {4, 0}, {7, 0}, {8, 0} };
edge_map[7] = { {3, 0}, {6, 0} };
edge_map[8] = { {4, 0}, {5, 0}, {6, 0} };
for (auto& i : edge_map) {
for (auto& j : i.second) {
G.add_edge(Edge<T>{ i.first, j.first, j.second });
}
}
return G;
}
template <typename T>
auto breadth_first_search(const Graph<T>& G, unsigned start) {
queue<unsigned> queue;
set<unsigned> visited; // 방문한 정점
vector<unsigned> visit_order; // 방문 순서
queue.push(start);
while (!queue.empty()) {
auto current_vertex = queue.front();
queue.pop();
// 현재 정점을 이전에 방문하지 않았다면
if (visited.find(current_vertex) == visited.end()) {
visited.insert(current_vertex);
visit_order.push_back(current_vertex);
for (auto& e : G.edges(current_vertex)) {
// 인접한 정점 중에서 방문하지 않은 정점이 있다면 큐에 추가
if (visited.find(e.dst) == visited.end()) {
queue.push(e.dst);
}
}
}
}
return visit_order;
}
int main() {
using T = unsigned;
// 그래프 객체 생성
auto G = create_reference_graph<T>();
cout << "[입력 그래프]" << endl;
cout << G << endl;
// 1번 정점부터 BFS 실행 & 방문 순서 출력
cout << "[BFS 방문 순서]" << endl;
auto bfs_visit_order = breadth_first_search(G, 1);
for (auto v : bfs_visit_order) {
cout << v << endl;
}
return 0;
}
결과
[입력 그래프]
1: {2: 0}, {5: 0},
2: {1: 0}, {5: 0}, {4: 0},
3: {4: 0}, {7: 0},
4: {2: 0}, {3: 0}, {5: 0}, {6: 0}, {8: 0},
5: {1: 0}, {2: 0}, {4: 0}, {8: 0},
6: {4: 0}, {7: 0}, {8: 0},
7: {3: 0}, {6: 0},
8: {4: 0}, {5: 0}, {6: 0},
[BFS 방문 순서]
1
2
5
4
8
3
6
7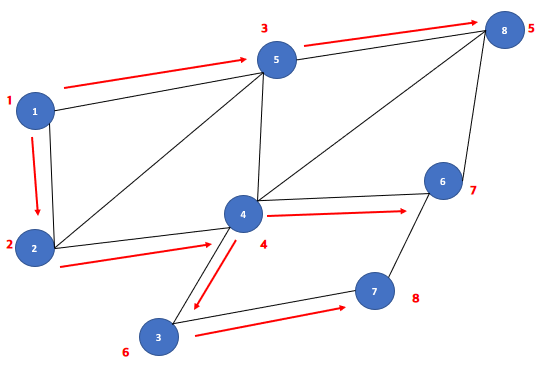
728x90
'Computer Science > Algorithm' 카테고리의 다른 글
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.07.02 |
|---|---|
| 다익스트라 최단 경로 알고리즘(Dijkstra Shortest Path Algorithm) (0) | 2021.06.30 |
| 프림의 최소 신장 트리 알고리즘(Prim's Minimum Spanning Tree Algorithm) (0) | 2021.06.30 |
| 깊이 우선 탐색(DFS, Depth-First Search) (0) | 2021.06.30 |
| 그래프 순회 문제(Graph Traversal Problem) ; 그래프 탐색 문제(Graph Search Problem) (0) | 2021.06.28 |
| 웰시-포웰 알고리즘(Welsh-Powell Algorithm) (0) | 2021.06.27 |
| 크루스칼 최소 신장 트리 알고리즘(Kruskal Minimum Spanning Tree Algorithm) (0) | 2021.06.26 |
| 분할 가능 배낭 문제(Fractional Knapsack Problem) (0) | 2021.06.25 |

