728x90
수학 계산
- 넘파이와 판다스 라이브러리는 과학 계산을 포함하는 데이터 분석에서 중요하게 사용된다.
- 넘파이는 ndarray 객체의 요소를 빠르게 계산할 수 있도록 강력한 기능을 가진 많은 함수를 제공한다.
- 넘파이와 판다스는 같은 플랫폼에서 설계되었으므로 넘파이의 함수들을 판다스에서도 그대로 사용할 수 있다.
- 판다스에서는 이러한 함수들을 사용해 메타 데이터를 제외한 시리즈와 데이터프레임의 데이터 구조에서 수학 계산을 쉽게 할 수 있다.
통계 함수
- 통계 함수에는 min(), max(), std(), var(), median(), count(), sum(), cumsum(), count(), prod() 등의 함수 외에도 pct_change(), cov(), corr(), rank() 함수가 있다.
퍼센트 변화율
- 시리즈와 데이터프레임에서 퍼센트 변화율(Percent Change)을 계산하기 전 pct_change()의 fill_method 인수를 이용해 NA나 Null 값을 채운다.
- 다음 예제에서는 주어진 수의 기간에 대한 퍼센트 변화율을 계산하기 위해 pct_change() 메소드를 적용한다.
>>> ser = pd.Series([1, 2, 3, 4, 5, 6]) >>> ser 0 1 1 2 2 3 3 4 4 5 5 6 dtype: int64 >>> ser.pct_change() 0 NaN 1 1.000000 2 0.500000 3 0.333333 4 0.250000 5 0.200000 dtype: float64
- 다음 예제에서 periods의 기본값은 1이다.
- ser 객체에 pct_change() 메소드를 적용하면 기준인 인덱스 0은 NaN이다.
- 인덱스 1 값은 ser 객체의 인덱스 0 값의 분모이며 인덱스 1에서 인덱스 0의 값을 뺀 값이 분자 값이다.
- 이때 분자가 0보다 크거나 같으면 +, 작으면 - 가 된다.
- periods=3 인수를 전달하여 실행한 후 퍼센트 변화율을 확인해본다.
>>> ser.pct_change(periods=3) 0 NaN 1 NaN 2 NaN 3 3.0 4 1.5 5 1.0 dtype: float64
- 앞 예제에서 periods=3은 이동 주기가 3이라는 뜻으로, ser 객체의 첫 3행이 NaN이 된다.
- ser 객체에 pct_change()를 적용해 인덱스가 3인 값을 구할 때 분모는 ser 객체의 인덱스 0의 값인 1이다.
- 분자는 ser 객체의 인덱스 3의 값인 4에서 인덱스 0의 값인 1을 뺀 값, 즉 3이 분자가 된다.
- 이후 값은 동일한 방식으로 구할 수 있다.
- 다음 예제에서 df 객체의 퍼센트 변화율을 구할 때 axis에 기본값과 columns 인수를 각각 전달한다.
- 인수 index의 값은 이산화탄소와 물의 화학식으로 첨자는 LaTex 표기법을 사용하였다.
df = pd.DataFrame( {'2021': [0.12, 0.24], '2022': [0.14, 0.26], '2023': [0.10, 0.22]}, index=['CO$_2$', 'H$_2$O']) df
df.pct_change()
df.pct_change(axis='columns')
공분산
- Series.cov() 함수는 시리즈 사이에서 손실 값을 제외한 공분산(Covariance)을 계산한다.
- 공분산 : 확률론과 통계학 분야에서 확률 변수 2개의 상관 정도를 나타내는 값
>>> ser1 = pd.Series(np.random.randn(100)) >>> ser2 = pd.Series(np.random.randn(100)) >>> ser1.cov(ser2) -0.02191981217711203
- DataFrame.cov() 함수는 데이터프레임 사이에서손실 값을 제외하고 쌍(Pair) 단위의 공분산을 계산한다.
df = pd.DataFrame(np.random.randn(1000, 3), columns=['a', 'b', 'c']) df.cov()
- DataFrame.cov()는 손실 값, null 값을 제외하고 열의 공분산 쌍을 구한다.
- 여기서 옵션인 min_periods 키워드는 유효한 결과값을 얻기 위해 열의 쌍당 요구되는 최소수의 관찰치를 뜻한다.
- 이것은 손실 값이 존재하는 데이터에서 정확한 결과를 얻기 위해 적용하는 인수이다.
df = pd.DataFrame(np.random.randn(10, 3), columns=['a', 'b', 'c']) df.loc[df.index[:3], 'a'] = np.nan df.loc[df.index[3:6], 'b'] = np.nan df.cov()
- 객체 df 에는 a 열에 3개, b 열에 3개의 손실 값이 존재한다.
- 손실 값이 공분산의 결과에 반영되지 않아 타당한 결과를 얻기 위해 각 열의 쌍에 대해 최소수인 관찰 값, 즉 min_periods 값을 인수로 전달해야 한다.
- 여기에서 총 관찰 수는 10개이고, 손실 값 수는 5개이다.
- 따라서 관찰 값의 최소수는 총 관찰 수 10개에서 손실 값 6개를 뺀 4개이므로, 이보다 큰 값에서 정한다.
df.cov(min_periods=5)
상관 관계
- 상관 계수(Correlation Coefficient)는 두 변량 사이의 상관 관계 정도를 의미하며, corr() 메소드로 상관 계수를 계산할 수 있다.
- 판다스에서는 corr() 메소드의 인수로 사용할 수 있는 몇몇 method를 제공한다.
| method | 기능 |
| pearson(기본) | 표준 상관 계수 |
| kendall | Kendall Tau 순위 상관 계수 |
| spearman | Spearman 상관 계수 |
- 상관 관계를 확인하기 위해 다음과 같이 df 객체를 생성하고 짝수 행에 손실 값을 할당한다.
df = pd.DataFrame(np.random.randn(500, 3), columns=['a', 'b', 'c']) df.iloc[::2] = np.nan df.head(6)
- df 에서 a 열과 b 열의 상관 계수를 구하고 df 열들의 쌍 단위(Pairwise) 상관 계수를 구한다.
- method='spearman'은 순위가 매겨진 두 변수 간 상관 관계를 계산하며, 통계학에서 주로 사용한다.
>>> df['a'].corr(df['b']) 0.038788059323480846 >>> df['a'].corr(df['b'], method='spearman') 0.0036223299572793167
df.corr()
- 상관 계수를 계산할 때 수치가 아닌 열들은 제외된다.
- 따라서 다음처럼 데이터프레임 열들의 쌍 단위에서 상관 계수를 구할 때는 NaN이 적용되지 않는다.
- 그러므로 min_periods 인수로 타당한 요소를 설정해야 df1에 있는 NaN이 적용된다.
df1 = pd.DataFrame(np.random.randn(20, 3), columns=['a', 'b', 'c']) df1.loc[df1.index[:5], 'a'] = np.nan df1.loc[df1.index[5:10], 'b'] = np.nan df1.corr()
df1.corr(min_periods=12)
- corrwith() 메소드는 두 데이터프레임 객체의 행들 또는 열들 사이의 쌍 단위 상관 계수를 구한다.
- 두 데이터프레임 객체들의 shape 가 다르면 NaN 값을 가진다.
>>> ind = ['a', 'b', 'c', 'd'] >>> col = ['one', 'two', 'three'] >>> df1 = pd.DataFrame(np.random.randn(4, 3), index=ind, columns=col) >>> df2 = pd.DataFrame(np.random.randn(3, 3), index=ind[:3], columns=col) >>> df1.corrwith(df2) one -0.056902 two -0.204342 three 0.697355 dtype: float64 >>> df2.corrwith(df1, axis=1) a -0.600366 b 0.767147 c 0.871352 d NaN dtype: float64
데이터 순위
- rank() 메소드는 시리즈나 데이터프레임에서 데이터의 순위(Ranking)을 구한다.
- 같은 값을 가지는 항목은 기본으로 평균값의 순위를 매긴다.
>>> ser = pd.Series(np.random.randn(5), index=list('abcde')) >>> ser a 0.896019 b -0.191600 c 0.560520 d -0.866108 e -0.734665 dtype: float64 >>> ser['d'] = ser['b'] >>> ser.rank() a 5.0 b 2.5 c 4.0 d 2.5 e 1.0 dtype: float64
- 데이터프레임에 rank() 메소드를 사용하면 행들(axis=0) 또는 열들(axis=1) 중 하나에 대해 순위를 매길 수 있다.
- NaN 값은 순위에서 제외된다.
df = pd.DataFrame(np.random.randn(5, 3)) df
>>> df[0][:2] 0 2.592567 1 -0.857084 Name: 0, dtype: float64
- 열 2에 df[0][:2] 를 동적 할당하고 순위를 구한다.
df[2] = df[0][:2] df
df.rank(1)
윈도우 함수
- 판다스는 데이터에서 window 나 rolling 등 기간을 이동하는 통계 자료를 계산할 수 있는 다양한 윈도우 함수를 제공한다.
- 윈도우 : 주어진 행과 떨어진 특정 행인 두 행 사이의 수
- 일반적으로 윈도우 함수들은 시간 순서를 가지는 시계열 데이터에서 평균값을 계산하는 데 많이 사용된다.
- 변화하는 트랜드를 윈도우 함수들을 통해 확인할 수 있기 때문이다.
- count(), sum(), mean(), median(), corr(), var(), cov(), std(), skew() 및 kurt() 가 윈도우 함수에 속한다.
- 판다스는 윈도우 계산을 위한 rolling() 메소드, 윈도우 확장 변환을 위한 expanding() 매소드, 지수 가중 이동 평균 계산을 ewm() 메소드를 제공한다.
- rolling()과 expanding() 메소드는 DataFrameGroupBy 객체에서 직접 사용할 수 있다.
>>> s = pd.Series(np.random.randn(1000), index=pd.date_range('1/1/2021', periods=1000)) >>> s 2021-01-01 -0.261559 2021-01-02 0.405811 2021-01-03 0.324935 2021-01-04 -1.937089 2021-01-05 0.969919 ... 2023-09-23 -0.531175 2023-09-24 -0.176443 2023-09-25 -0.409004 2023-09-26 -0.631045 2023-09-27 0.780370 Freq: D, Length: 1000, dtype: float64
- 시리즈 객체 s에 누적 합을 계산하는 cumsum() 함수를 적용한다.
>>> ser = s.cumsum() >>> ser 2021-01-01 -0.261559 2021-01-02 0.144253 2021-01-03 0.469188 2021-01-04 -1.467901 2021-01-05 -0.497982 ... 2023-09-23 -33.698439 2023-09-24 -33.874882 2023-09-25 -34.283886 2023-09-26 -34.914931 2023-09-27 -34.134561 Freq: D, Length: 1000, dtype: float64
- 시리즈 객체 s에 rolling() 메소드를 적용하고 인수 window=60 을 전달한다.
- Rolling 객체에 속한 여러 메소드와 속성은 roll. 을 타이핑한 후 <Tab> 키를 누르면 확인할 수 있으며, 이 메소드들은 모두 호출할 수 있다.
- 다음 예제에서는 1천 개 행으로 이루어진 s 객체 데이터에서 첫 번째 60개 행의 평균값을 roll, mean() 메소드로 계산한다.
- 결과 데이터의 60번째 행에 첫 번째 연산 결과를 나타내고 0부터 59번째 행은 NaN 으로 처리한다.
- 또한 전체 데이터의 2번째 행부터 61번째 행까지 평균값을 연산하는 결과를 61번째 행에 나타낸다.
- 이러한 방법으로 1천 개 행의 변화하는 평균값을 구할 수 있다.
>>> roll = s.rolling(window=60) >>> roll Rolling [window=60,center=False,axis=0] >>> type(roll) pandas.core.window.rolling.Rolling >>> roll.mean() 2021-01-01 NaN 2021-01-02 NaN 2021-01-03 NaN 2021-01-04 NaN 2021-01-05 NaN ... 2023-09-23 -0.033356 2023-09-24 -0.031705 2023-09-25 -0.033527 2023-09-26 -0.047816 2023-09-27 0.005777 Freq: D, Length: 1000, dtype: float64
- rolling() 메소드를 실행하면 라벨은 기본으로 윈도우의 오른쪽 테두리에 설정된다.
- center=True 로 설정하면 윈도우의 중심으로 라벨의 위치를 변경할 수 있다.
- Rolling 객체는 통계를 계산하는 다음과 같은 메소드를 지원한다.
| 메소드 종류 | 기능 |
| count() | null 이 아닌 관찰치의 수 |
| sum() | 값들의 합 |
| mean() | 값들의 평균 |
| median() | 중앙값 |
| min() | 최솟값 |
| max() | 최댓값 |
| std() | Bessel 보정의 표본 표준 편차 |
| var() | 편향되지 않는(Unbiased) 분산 |
| skew() | 표본 왜도(Sample Skewness) |
| kurt() | 표본 첨도(Sample Kurtosis) |
| quantile() | 표본 분위수(Sample Quantile)로 %로 표기되는 값 |
| apply() | 일반적인 적용 |
| cov() | 편향되지 않는 공분산 (binary) |
| corr() | 상관 계수 (binary) |
- 시리즈에 cumsum() 메소드를 이용해 누적 합을 계산한 ser 을 그래프로 그려본다.
ser.plot(style='k')
- 이번에는 데이터프레임 객체에 cumsum() 메소드를 적용하고, 이 결과에 window=60 인 rolling() 메소드 연산 후 sum() 연산을 실행한다.
- 그리고 결과 데이터 3개 열의 그래프를 최종 반환한다.
- 먼저 다음과 같이 데이터프레임을 생성한다.
df = pd.DataFrame(np.random.randn(1000, 3), index=pd.date_range('1/1/2021', periods=1000), columns=['A', 'B', 'C']) df
- 데이터프레임 객체 df에 cumsum() 메소드를 적용해 열 방향 누적 합을 구한다.
dfc = df.cumsum() dfc
- 데이터프레임 객체 dfc에 window=60 인 rolling() 메소드 그리고 sum() 함수를 적용한다.
dfc.rolling(window=60).sum()
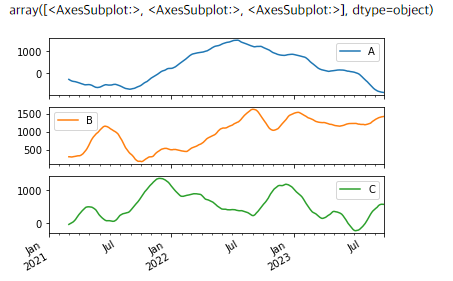
- 최종 연산 결과를 그래프로 나타낸다.
dfc.rolling(window=60).sum().plot(subplots=True)
- 이번에는 이동 합계를 구하기 위한 시리즈 객체를 다음과 같이 생성한다.
>>> ser = pd.Series([1, 2, 3, 4, 5]) >>> ser 0 1 1 2 2 3 3 4 4 5 dtype: int64
- window=3 인 이동 합계를 구한다.
- center=True 를 입력하면 윈도우 중심에서 라벨을 설정한다.
- 이것은 NaN 값을 처음과 마지막 부분에 배치한다는 의미로, 윈도우가 3이면 맨 처음과 마지막 값이 NaN 이 된다.
>>> ser.rolling(3).sum() 0 NaN 1 NaN 2 6.0 3 9.0 4 12.0 dtype: float64 >>> ser.rolling(3, center=True).sum() 0 NaN 1 6.0 2 9.0 3 12.0 4 NaN dtype: float64
시간 인식 이동
- 시간 인식 이동(Time-Aware Rolling)은 rolling() 메소드에 오프셋이나 이에 동등한 것을 전달하고 이를 기반으로 다양한 크기의 윈도우를 가질 수 있도록 해야 한다.
- 이렇게 하면 지정한 시간 구간 내에서 발생하는 모든 선행 값들을 포함한다.
- 시간 인식 이동을 예제를 통해 확인해보기 위해 우선 데이터프레임 객체 dfc를 생성한다.
dft = pd.DataFrame({'val': [0, 1, 2, np.nan, 4]}, index=pd.date_range('20210101 09:00:00', periods=5, freq='s')) dft
- 위의 연산 결과는 규치적인 도수 인덱스를 가진다.
- 다음과 같이 윈도우 매개 변수로 정수를 사용하는 것은 윈도우 도수에 따라 이동시킨다는 의미이다.
dft.rolling(2).sum()
- 윈도우가 2이고, NaN이 1개이므로 sum() 연산으로 유효한 값을 얻기 위해 min_periods 를 1로 설정했다.
dft.rolling(2, min_periods=1).sum()
- window 함수에 전달한 오프셋 '2s'는 시간 간격을 의미한다.
- 윈도우를 2초 단위로 나누어 계산한다는 뜻이다.
- 이러한 방식으로 오프셋을 입력하는 것은 이동 도수를 더 직관적인 규격으로 설정하는 것이다.
dft.rolling('2s').sum()
- 다음 예제에서는 단조(Monotonic) 인덱스를 가지는 dft1의 이동 합계를 계산한다.
- 단조는 변화가 없거나 일정함을 의미한다.
dft1 = pd.DataFrame({'val': [0, 1, 2, np.nan, 4]}, index=pd.Index([pd.Timestamp('20210101 09:00:00'), pd.Timestamp('20210101 09:00:01'), pd.Timestamp('20210101 09:00:02'), pd.Timestamp('20210101 09:00:03'), pd.Timestamp('20210101 09:00:04')], name='ha')) dft1
dft1.rolling(2).sum()
- 오프셋에 시간 규격을 설정하면 데이터에서 변화하는 윈도우를 생성한다.
dft1.rolling('2s').sum()
- on 매개 변수를 전달하면 데이터프레임 열에 윈도우 함수를 적용할 수 있다.
dft2 = dft1.reset_index() dft2
dft2.rolling('2s', on='ha').sum()
이진 윈도우 함수
- cov() 와 corr() 함수는 2개의 시리즈 조합이나 데이터프레임과 시리즈 조합 또는 2개의 데이터프레임 조합에서 이동 윈도우 통계를 계산할 수 있으며, 다음과 같이 연산을 수행한다.
- 시리즈와 시리즈 : 쌍의 통계를 계산한다.
- 데이터프레임과 시리즈 : 데이터프레임에 시리즈를 전달해 데이터프레임 각 열의 통계를 계산하고 데이터프레임을 반환한다.
- 데이터프레임과 데이터프레임
- 열 이름에 매칭하는 통계를 계산하고 기본으로 데이터프레임을 반환한다.
- 키워드 인수 pairwise=True 를 전달하면 각 열의 쌍에 대한 통계를 계산하고 멀티 인덱스로 이루어진 데이터프레임을 반환한다.
- 앞 3가지 연산을 예제를 통해 확인해본다.
df = pd.DataFrame(np.random.randn(500, 3), index=pd.date_range('1/1/2021', periods=500), columns=['A', 'B', 'C']) dfc = df.cumsum() dfc.head()
- df1 객체를 생성하고 dfc 객체에서 20개 행을 df1 객체에 할당한다.
df1 = dfc[:20] df1.head()
- df1 객체에 window=5 인수를 갖는 rolling() 함수를 적용하고 df1['B'] 와의 상관 관계를 구한다.
df1.rolling(window=5).corr(df1['B'])
쌍 단위의 공분산과 상관 관계를 이동 윈도우로 계산하기
- 금융 데이터 분석 분야 등에서는 시계열 모음의 공분산과 상관 관계 매트릭스 계산을 이용한다.
- 상관 관계 매트릭스 : 변수 사이에서 상관 계수를 나타내는 테이블
- 이동 윈도우 공분산과 상관 관계는 pairwise 키워드 인수를 전달해 계산할 수 있다.
- 데이터프레임을 입력하면 멀티 인덱스로 이루어진 데이터프레임이 결과로 나타난다.
- 이때 인덱스는 날짜이며, 단일 데이터프레임에서 pairwise 인수는 생략할 수 있다.
- 다음 예제에서는 df 객체의 B와 C 열 요소에 rolling() 함수를 적용하고 A와 B열 요소의 공분산을 구한다.
cvar = (df[['B', 'C']].rolling(window=50).cov(df[['A', 'B']], pairwise=True)) cvar
- loc 속성으로 2022년 5월 13일부터 2022년 5월 15일까지의 요소로 이루어진 데이터프레임 객체를 구한다.
cvar.loc['2022-05-13':]
- 다음으로 df 객체에 rolling() 함수를 적용한 후 상관 관계를 구한다.
- 이 결과에 loc 메소드를 적용해 2022년 5월 13일부터 2022년 5월 15일까지 요소로 이루어진 데이터프레임 객체를 구한다.
dfr = df.rolling(window=50).corr() dfr.loc['2022-05-13':]
- 재형성과 인덱스를 이용하면 2개 열 사이에서 시계열의 상관 관계를 효율적으로 검색할 수 있다.
- 예제에서는 unstack() 메소드를 적용한다.
dfr.unstack().tail(3)
- df.unstack() 객체에서 요소가 ('A', 'C')인 객체를 구하고, 마지막 3행을 반환하는 객체를 다음과 같이 구한다.
>>> dfr.unstack()[('A', 'C')] 2021-01-01 NaN 2021-01-02 NaN 2021-01-03 NaN 2021-01-04 NaN 2021-01-05 NaN ... 2022-05-11 -0.015247 2022-05-12 -0.028359 2022-05-13 -0.024734 2022-05-14 -0.035496 2022-05-15 -0.051418 Name: (A, C), Length: 500, dtype: float64 >>> dfr.unstack()[('A', 'C')].tail(3) 2022-05-13 -0.024734 2022-05-14 -0.035496 2022-05-15 -0.051418 Name: (A, C), dtype: float64
- 시리즈 객체 dfr.unstack()[('A', 'C')] 를 그래프로 나타낸다.
dfr.unstack()[('A', 'C')].plot()
집계 연산
- Rolling 객체를 생성하면 여러 메소드를 이용해 데이터에서 하나 이상의 계산을 수행할 수 있다.
- 이렇게 여러 메소드를 적용하는 데이터 집계는 aggregate() 메소드를 사용하는 방법과 유사하다.
- Rolling 객체에 aggregate() 메소드를 적용하는 예제는 다음과 같다.
df = pd.DataFrame(np.random.randn(1000, 3), index=pd.date_range('1/1/2021', periods=1000), columns=['A', 'B', 'C']) df
>>> rol = df.rolling(window=60, min_periods=1) >>> rol Rolling [window=60,min_periods=1,center=False,axis=0]
- 생성한 rol 객체에 aggregate() 메소드를 적용하고 numpy.sum 함수를 인수로 전달하여 연산 결과를 집계한다.
- 또한 A 열에 연산을 실행하고, A와 C열에 동일하게 연산을 실행한다.
rol.aggregate(np.sum)
>>> rol['A'].aggregate(np.sum) 2021-01-01 0.335989 2021-01-02 0.640379 2021-01-03 0.057467 2021-01-04 1.053226 2021-01-05 1.990919 ... 2023-09-23 8.433061 2023-09-24 6.484539 2023-09-25 6.387734 2023-09-26 6.094186 2023-09-27 5.838368 Freq: D, Name: A, Length: 1000, dtype: float64
rol[['A', 'C']].agg(np.sum)
복수의 함수를 적용하기
- 윈도우가 적용된 시리즈에 집계 연산을 실행하기 위해 함수들을 전달할 수 있다.
- 이때 결과로 데이터프레임을 반환한다.
rol['A'].agg([np.sum, np.mean, np.std])
- 윈도우가 적용된 데이터프레임의 각 열에 집계 연산을 실행하기 위해 함수들을 전달할 수 있다.
- 이때 멀티 인덱스를 갖는 집계 결과를 반환한다.
rol[['A', 'C']].agg([np.sum, np.mean])
데이터프레임 열들에 여러 함수를 적용하기
- 데이터프레임 열들에 함수를 딕셔너리로 전달하면 집계 연산을 수행할 수 있다.
- ddof 옵션은 델타 자유도를 설정하며 기본값은 0이다.
- ddof=1 은 n-1로 표준 편차를 계산하라는 의미이다.
rol.agg({'A': np.sum, 'C': lambda x: np.std(x, ddof=1)})
- 문자열로 된 함수 이름을 사용해 연산을 실행할 수 있다.
- 이때 윈도우가 적용된 객체에서 연산을 실행해야 문자열이 유효하다.
rol.agg({'A': 'sum', 'C': 'std'})
- 중첩된 딕셔너리를 전달하면 행에 여러 집계 연산을 지정할 수 있다.
rol.agg({'A': ['sum', 'std'], 'C': ['mean', 'std']})
기타 윈도우 적용
확장 윈도우
- 확장 윈도우(Expanding Window)를 적용하면 해당 시간 시점까지 사용 가능한 모든 데이터를 이용해 값을 산출한다.
- 이때 expanding() 메소드를 이용한다.
- 다음 예제에서는 rolling() 메소드에 df의 전체 요소 수를 설정하고 expanding() 메소드를 적용한다.
- Rolling 객체에서 사용하는 메소드들을 expanding() 메소드에서도 사용할 수 있다.
- 먼저 rolling() 메소드 연산을 실행한 후, expanding() 메소드 연산 결과와 비교해본다.
df = pd.DataFrame(np.random.randn(100, 3), index=pd.date_range('7/1/2021', periods=100), columns=['A', 'B', 'C']) df.rolling(window=len(df), min_periods=1).mean()[:5]
- 다음 예제에서는 expanding() 메소드를 사용하여 1개 행 단위로 열 방향 평균을 구한다.
- min_periods=1은 기본값으로써 첫 행부터 관찰한다는 의미이며 min_periods=2 인 경우 첫 행은 관찰하지 않으므로 NaN으로 처리된다.
>>> df.expanding(min_periods=1) Expanding [min_periods=1,center=False,axis=0]
df.expanding(min_periods=1).mean()[:5]
- 다음 예제에서는 시리즈 객체를 생성해 expanding() 메소드와 cumsum() 메소드를 적용하고 결과를 비교한다.
>>> ser = pd.Series([1, 2, np.nan, 3, np.nan, 4]) >>> ser.expanding().sum() 0 1.0 1 3.0 2 3.0 3 6.0 4 6.0 5 10.0 dtype: float64 >>> ser.cumsum() 0 1.0 1 3.0 2 NaN 3 6.0 4 NaN 5 10.0 dtype: float64 >>> ser.cumsum().fillna(method='ffill') 0 1.0 1 3.0 2 3.0 3 6.0 4 6.0 5 10.0 dtype: float64
- rolling() 에서는 윈도우가 일정하게 유지되는 반면 expanding() 에서는 윈도우가 변화한다.
- 예를 들면, 윈도우가 60인 이동 윈도우는 계속 이동하면서 크기가 일정하다.
- 그러나 확장 윈도우를 mean() 과 함께 연산하는 경우 1행→2행, 1행→3행 등으로 계속 확장하면서 연산한다.
df = pd.DataFrame({'A' : [1, 2, 3, 4, 5, 6, 7]}, index=pd.date_range('7/1/2021', periods=7)) df
df.expanding(min_periods=2).mean()
df.rolling(window=2).mean()
- 이동 윈도우 통계보다 확장 윈도우 통계가 더 안정적이다.
- 다음 예제에서 시리즈 객체를 생성한 후, rolling() 메소드와 expanding() 메소드를 이용한 연산 결과를 그래프로 확인한다.
s = pd.Series(np.random.randn(1000), index=pd.date_range('1/1/2021', periods=1000)) ser = s.cumsum() rol = ser.rolling(window=60)
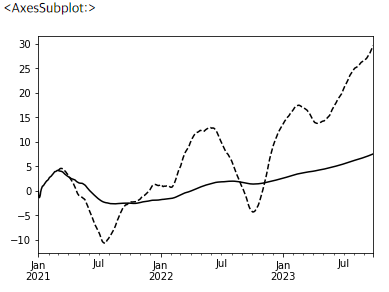
- 생성된 시리즈 객체 ser을 그래프로 나타내 비교한다.
rol.mean().plot(style='k--') ser.expanding().mean().plot(style='k')
지수 가중 윈도우
- rolling(), expanding(), ewm() 메소드를 사용하면 윈도우 객체를 반환한다.
- ewm() 메소드는 지수적으로 이동하는 윈도우 객체를 얻기 위해 다음과 같은 함수들을 제공한다.
| 함수 | 기능 |
| mean() | 지수 가중 이동 평균 |
| var() | 지수 가중 이동 분산 |
| std() | 지수 가중 이동 표준 편차 |
| corr() | 지수 가중 이동 상관 관계 |
| cov() | 지수 가중 이동 공분산 |
- 지수 가중 윈도우의 통계 이론은 내용이 방대하므로 이 페이지에서는 생략하고 평균을 구하는 간단한 연산만 실행하여 이동 윈도우 평균과 비교하는 그래프를 그린다.
ser.ewm(span=20).mean().plot(style='k') rol.mean().plot(style='k--')
728x90
'In-depth Study > Pandas' 카테고리의 다른 글
| [Pandas] 데이터의 그룹 연산 (0) | 2022.05.30 |
|---|---|
| [Pandas] 데이터 가공 (0) | 2022.05.29 |
| [Pandas] 데이터 타입과 입출력 (0) | 2022.05.27 |
| [Pandas] 데이터 처리 (0) | 2022.05.27 |
| [Pandas] 판다스의 주요 기능 (0) | 2022.05.25 |
| [Pandas] 판다스 데이터 구조 (1) | 2022.05.24 |
| [Pandas] 판다스(Pandas) 개요 (0) | 2022.05.24 |