728x90
삼각 함수(Trigonometrical Function)
삼각 함수
- 각에 대한 함수로서 삼각형의 각과 변의 길이를 연관시킨 것
- 삼각형의 연구뿐만 아니라 소리나 빛의 파동과 같은 다양한 주기적 현상을 설명하는 데 이용된다.
- 정의 방법
- 직각 삼각형의 변의 길이의 비
- 좌표평면 위의 원에서 얻어지는 다양한 선분의 길이
- 무한 급수 (최근)
- 복소수의 값을 취하는 경우까지 확장
- 종류 : 사인(Sine) 함수, 코사인(Cosine) 함수, 탄젠트(Tangent) 함수
① 직각 삼각형(Right Triangle)에서의 삼각 함수
- $\angle C$ 가 직각인 직각 삼각형에서, $\angle A$, $\angle B$, $\angle C$ 와 마주 보는 변의 길이를 $a, b, c$ 라고 할 때, $\angle A$ 에 대한 사인(Sine), 코사인(Cosine), 탄젠트(Tangent)는 다음과 같이 정의한다.
$sin A = \frac{대변}{빗변} = \frac{a}{c}$
$cos A= \frac{인접변}{빗변} = \frac{b}{c}$
$tan A = \frac{대변}{인접변} = \frac{a}{b}$
- 위 세 함수의 역수를 $\angle A$ 에 대한 코시선트(Cosecant), 시컨트(Secant), 코탄젠트(Cotangent)라 하고, 다음과 같이 나타낸다.
$csc A= \frac{빗변}{대변} = \frac{c}{a}$
$sec A= \frac{빗변}{인접변} = \frac{c}{b}$
$cot A = \frac{인접변}{대변} = \frac{b}{a}$
- 다음의 사실을 이용하면 다음과 같은 결과를 얻게 된다.
- 세 각의 크기가 각각 45˚, 45˚, 90˚인 직각 삼각형은 이등변 삼각형이다.
- 세 각의 크기가 각각 30˚, 60˚, 90˚인 직각 삼각형의 빗변의 길이는 가장 짧은 변의 길이의 2배이다.
- 피타고라스 정리 : $c^{2} = a^{2} + b^{2}$
■ 삼각 함수 특수각 표
함수 \ 각도 0˚ 30˚ 45˚ 60˚ 90˚ sin $0$ $\frac{1}{2}$ $\frac{\sqrt{2}}{2}(\frac{1}{\sqrt{2}}$) $\frac{\sqrt{3}}{2}$ $1$ cos $1$ $\frac{\sqrt{3}}{2}$ $\frac{\sqrt{2}}{2}(\frac{1}{\sqrt{2}}$) $\frac{1}{2}$ $0$ tan $0$ $\frac{\sqrt{3}}{3}(\frac{1}{\sqrt{3}})$ $1$ $\sqrt{3}$ $∞$
② 일반각에 대한 삼각 함수
- 직각 삼각형의 각은 0˚와 90˚ 사이에 있으므로, 위의 직각 삼각형에 대한 삼각 함수는 음의 각이나 90˚보다 큰 각에 대해서는 적용되지 않는다.
- 삼각 함수를 일반각으로 확장하기 위해서는 좌표 평면 위의 한 원을 살펴보는 것이 편리하다.
- $xy$ 좌표 평면에서 원점 $O$ 를 중심으로 하고, 반지름의 길이가 $r$ 인 원이 있을 때,
- 윈 위의 점 $P(x, y)$ 에 대해 동경 $OP$ 가 $x$ 축과 이루는 각의 크기를 $\theta$ 라고 하면, 위의 여섯 개의 삼각 함수는 다음과 같이 정의된다.
$sin\theta = \frac{y}{r}$ $cos\theta = \frac{x}{r}$ $tan\theta = \frac{y}{x}$ $csc\theta = \frac{r}{y}$ $sec\theta = \frac{r}{x}$ $cot\theta = \frac{x}{y}$
③ 삼각 항등식(Trigonometric Identity)
- 삼각 함수에 관한 방정식으로서 양변이 모든 각에 대해 항상 성립하는 항등식을 뜻한다.
- 대표적인 삼각 항등식은 피타고라스 정리를 응용한 것이다.
$$x^{2} + y^{2} = r^{2}$$
- 이 식의 양변을 $r^{2}$ 으로 나누면, 사인과 코사인의 정의를 이용하여 다음을 얻게 된다.
$$sin^{2}\theta + cos^{2}\theta = 1$$
- 다시 이 식을 각각 $cos^{2}\theta, sin^{2}\theta$ 로 나누면 다음을 얻는다.
$$tan^{2}\theta + 1 = sec^{2}\theta$$
$$1 + cot^{2}\theta = csc^{2}\theta$$
- 한편, 점 $(x, y)$ 가 단위원 위의 점이면 $(-x, y), (-x, -y), (x, -y)$ 도 단위원 위의 점이다.
- 이 네 점은 각 변이 좌표 축과 평행한 직사각형의 네 꼭짓점이다.
- 특히, 이 꼭짓점의 $x$좌표와 $y$좌표는 그 대응하는 각의 코사인과 사인이다.
- 따라서 다음 등식을 얻게 된다.
$sin(\pi - \theta) = sin\theta$ $sin(\pi + \theta) = -sin\theta$ $sin(-\theta) = -sin\theta$ $cos(\pi - \theta) = -cos\theta$ $cos(\pi + \theta) = -cos\theta$ $cos(-\theta) = cos\theta$ $tan(\pi - \theta) = -tan\theta$ $tan(\pi + \theta) = tan\theta$ $tan(-\theta) = -tan\theta$
(참고) 시뮬레이터
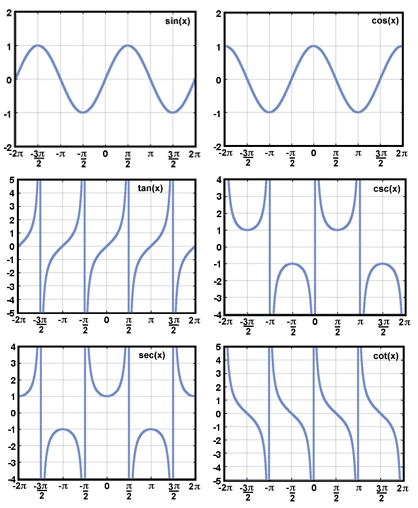
(참고) 그래프
728x90
